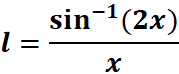
# 1st: Import the sympy module
import sympy as sp  # Import sympy for symbolic mathematics

# 2nd: Define the variable
x = sp.symbols('x')  # Define 'x' as a symbolic variable

# 3rd: Define the function l(x)
l = sp.asin(2*x) / x  # Define the function l(x) = asin(2x) / x

# 4th: Differentiate l(x) with respect to x
derivative = sp.diff(l, x)  # Find the derivative of l(x) with respect to x

# 5th: Print the result
print("Function l(x):", l)  # Output the function l(x)
print("Derivative dl/dx:", derivative.simplify())  # Output the simplified derivative of l(x)

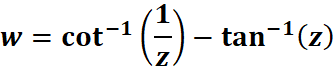
# 1st: Import the sympy module
import sympy as sp  # Import sympy for symbolic mathematics

# 2nd: Define the variable
z = sp.symbols('z')  # Define 'z' as a symbolic variable

# 3rd: Define the function w(z)
w = sp.atan(1/z) - sp.atan(z)  # Define the function w(z) = atan(1/z) - atan(z)

# 4th: Differentiate w(z) with respect to z
derivative = sp.diff(w, z)  # Find the derivative of w(z) with respect to z

# 5th: Print the result
print("Function w(z):", w)  # Output the function w(z)
print("Derivative dw/dz:", derivative.simplify())  # Output the simplified derivative of w(z)

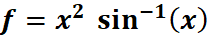
# 1st: Import the sympy module
import sympy as sp  # Import sympy for symbolic mathematics

# 2nd: Define the variable
x = sp.symbols('x')  # Define 'x' as a symbolic variable

# 3rd: Define the function f(x)
f = x**2 * sp.asin(x)  # Define the function f(x) = x^2 * asin(x)

# 4th: Differentiate f(x) with respect to x
derivative = sp.diff(f, x)  # Find the derivative of f(x) with respect to x

# 5th: Print the result
print("Function f(x):", f)  # Output the function f(x)
print("Derivative df/dx:", derivative)  # Output the derivative of f(x)

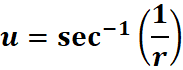
# 1st: Import the sympy module
import sympy as sp  # Import sympy for symbolic mathematics

# 2nd: Define the variable
r = sp.symbols('r')  # Define 'r' as a symbolic variable

# 3rd: Define the function u(r)
u = sp.acos(1/r)  # Define the function u(r) = acos(1/r)

# 4th: Differentiate u(r) with respect to r
derivative = sp.diff(u, r)  # Find the derivative of u(r) with respect to r

# 5th: Print the result
print("Function u(r):", u)  # Output the function u(r)
print("Derivative du/dr:", derivative)  # Output the derivative of u(r)

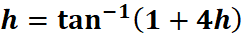
# 1st: Import the sympy module
import sympy as sp  # Import sympy for symbolic mathematics

# 2nd: Define the variable
h = sp.symbols('h')  # Define 'h' as a symbolic variable

# 3rd: Define the function h(h)
function = sp.atan(1 + 4*h)  # Define the function h(h) = atan(1 + 4h)

# 4th: Differentiate h(h) with respect to h
derivative = sp.diff(function, h)  # Find the derivative of h(h) with respect to h

# 5th: Print the result
print("Function h(h):", function)  # Output the function h(h)
print("Derivative dh/dh:", derivative)  # Output the derivative of h(h)