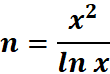
# 1st: Import the sympy module
import sympy as sp  # Import sympy for symbolic mathematics

# 2nd: Define the variable
x = sp.symbols('x')  # Define 'x' as a symbolic variable

# 3rd: Define the function n
n = x**2 / sp.ln(x)  # Define the function n(x) = x^2 / ln(x)

# 4th: Calculate the derivative
derivative_n = sp.diff(n, x)  # Calculate the derivative of n with respect to x

# 5th: Display the result
print("The derivative of n with respect to x is:", derivative_n)  # Output the derivative of n

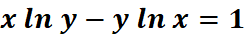
# 1st: Import the sympy module
import sympy as sp  # Import sympy for symbolic mathematics

# 2nd: Define the variables
x, y = sp.symbols('x y')  # Define 'x' and 'y' as symbolic variables

# 3rd: Define the implicit equation
equation = x * sp.ln(y) - y * sp.ln(x) - 1  # Define the implicit equation

# 4th: Differentiate the equation implicitly with respect to x
dy_dx = sp.diff(equation, x) + sp.diff(equation, y) * sp.Derivative(y, x)  
# Use implicit differentiation

# 5th: Solve for dy/dx
dy_dx_solution = sp.solve(dy_dx, sp.Derivative(y, x))[0]  # Solve the equation for dy/dx

# 6th: Display the result
print("The derivative dy/dx is:", dy_dx_solution)  # Output the derivative dy/dx

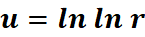
# 1st: Import the sympy module
import sympy as sp  # Import sympy for symbolic mathematics

# 2nd: Define the variable
r = sp.symbols('r')  # Define 'r' as a symbolic variable

# 3rd: Define the function u
u = sp.ln(sp.ln(r))  # Define the function u(r) = ln(ln(r))

# 4th: Differentiate u with respect to r
du_dr = sp.diff(u, r)  # Find the derivative of u(r) with respect to r

# 5th: Display the result
print("The derivative of u with respect to r is:", du_dr)  # Output the derivative du/dr

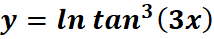
# 1st: Import the sympy module
import sympy as sp  # Import sympy for symbolic mathematics

# 2nd: Define the variable
x = sp.symbols('x')  # Define 'x' as a symbolic variable

# 3rd: Define the function y
y = sp.ln(sp.tan(3*x)**3)  # Define y = ln(tan(3x)^3)

# 4th: Differentiate y with respect to x
dy_dx = sp.diff(y, x)  # Find the derivative of y with respect to x

# 5th: Display the result
print("The derivative of y with respect to x is:", dy_dx)  # Output the derivative dy/dx

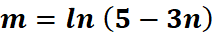
# 1st: Import the sympy module
import sympy as sp  # Import sympy for symbolic mathematics

# 2nd: Define the variable
n = sp.symbols('n')  # Define 'n' as a symbolic variable

# 3rd: Define the function m
m = sp.ln(5 - 3*n)  # Define m = ln(5 - 3n)

# 4th: Differentiate m with respect to n
dm_dn = sp.diff(m, n)  # Find the derivative of m with respect to n

# 5th: Display the result
print("The derivative of m with respect to n is:", dm_dn)  # Output the derivative dm/dn