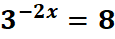
# 1st: Import the sympy module
import sympy as sp  # Import sympy for symbolic mathematics

# 2nd: Define the constants
ln_2 = sp.ln(2)  # Define ln(2)
ln_3 = sp.ln(3)  # Define ln(3)

# 3rd: Calculate ln(8)
ln_8 = 3 * ln_2  # Since 8 = 2^3

# 4th: Define the equation for x
x = - (ln_8 / (2 * ln_3))  # Define the equation x = - (1/2) * (ln(8) / ln(3))

# 5th: Print the equation and the solution
print("Equation: x = - (1/2) * (ln(8) / ln(3))")  # Output the equation
print("Value of x:", x.evalf())  # Output the value of x

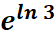
# 1st: Import the sympy module
import sympy as sp  # Import sympy for symbolic mathematics

# 2nd: Define the variable
a = 3  # Define the value of 'a'

# 3rd: Express the equation
# The equation is simply e^(ln(3))
equation = sp.exp(sp.ln(a))  # Exponentiate the natural logarithm of 'a'

# 4th: Find the value of x
solution = equation  # The solution is the evaluated equation

# 5th: Print the equation and the solution
print("Equation in symbolic form: e^(ln(3))")  # Output the equation
print("Solution for x:", solution)  # Output the solution for x

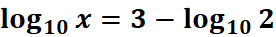
# 1st: Import the sympy module
import sympy as sp  # Import sympy for symbolic mathematics

# 2nd: Define the variable
x = sp.symbols('x')  # Define 'x' as a symbolic variable

# 3rd: Express the equation
# log10(x) = 3 - log10(2)
equation = sp.log(x, 10) - (3 - sp.log(2, 10))  # Define the equation log10(x) = 3 - log10(2)

# 4th: Solve for x
solution = sp.solve(equation, x)  # Solve the equation for x

# 5th: Print the equation and the solution
print("Equation in symbolic form:", equation)  # Output the equation in symbolic form
print("Solution for x:", solution[0])  # Output the solution for x

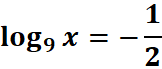
# 1st: Import the sympy module
import sympy as sp  # Import sympy for symbolic mathematics

# 2nd: Define the variable
x = sp.symbols('x')  # Define 'x' as a symbolic variable

# 3rd: Express the equation
# log_9(x) = -1/2 can be rewritten using the change of base formula
equation = sp.log(x, 9) + 1/2  # Define the equation log_9(x) = -1/2

# 4th: Solve for x
solution = sp.solve(equation, x)  # Solve the equation for x

# 5th: Print the equation and the solution
print("Equation in symbolic form:", equation)  # Output the equation in symbolic form
print("Solution for x:", solution[0])  # Output the solution for x

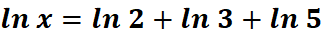
# 1st: Import the sympy module
import sympy as sp  # Import sympy for symbolic mathematics

# 2nd: Define the variable
x = sp.symbols('x')  # Define 'x' as a symbolic variable

# 3rd: Express the equation
# ln(x) = ln(2) + ln(3) + ln(5)
equation = sp.ln(x) - (sp.ln(2) + sp.ln(3) + sp.ln(5))  # Define the equation

# 4th: Solve for x
solution = sp.solve(equation, x)  # Solve the equation for x

# 5th: Print the equation and the solution
print("Equation in symbolic form:", equation)  # Output the equation in symbolic form
print("Solution for x:", solution[0])  # Output the solution for x