Definition
Trigonometric Function
-> The mathematical process of rate at which the value of the function changes with respect to its input variable.
Formulas of Trigonometric Functions |
1. Sine Derivative
-> This means that the rate of change of the sine function with respect to ? is given by the cosine of ?.
Formula: y = f(x) = sin(x)
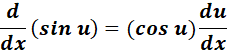
2. Cosine Derivative
-> The derivative of the cosine function with respect to ? is equal to the negative of the sine of ?.
Formula: y = f(x) = cos(x)
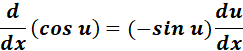
3. Tangent Derivative
-> The derivative of the tangent function with respect to ? is the secant squared of ?.
Formula: y = f(x) = tan(x)
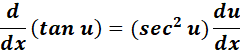
4. Cotengent Derivative
-> The derivative of the cotangent function with respect to ? is negative cosecant squared of ?.
Formula: y = f(x) = cot(x)
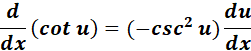
5. Secant Derivative
-> The derivative of the secant function with respect to ? is equal to secant of ? times tangent of ?.
Formula: y = f(x) = sec(x)
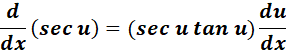
6. Cosecant Derivative
-> The derivative of the cosecant function with respect to ? is equal to negative cosecant of ? times cotangent of ?.
Formula: y = f(x) = csc(x)
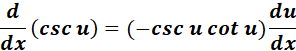
Example |
1. Find the answer from this given:
y = sin 3x
Steps:
a. Write the d/dx first.
b. Use the specific derivative formula.
c. Find the dy/dx.
= y = sin 3x
= 
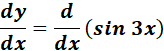
= x = 3x; dx = 3
= 
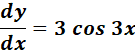
= 3 cos 3x
Exercises |
1. v = 3 cos 2u
Steps:
a. Write the dv/du first.
b. Use the specific derivative formula.
c. Find the dv/du.
Solution:
= v = 3 cos 2u
= Formula: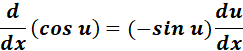
= 
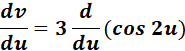
= u = 2u; du = 2
= 
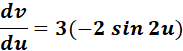
= -6 sin 2u
Answer: -6 sin 2u
2. y = sin 3x5
Steps:
a. Write the dy/dx first.
b. Use the specific derivative formula.
c. Find the dy/dx.
Solution:
= y = sin 3x5
= Formula: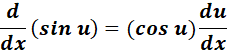
= 
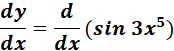
= x = 3x5; dx = 15x4
= 
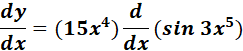
= 15x4 cos 3x5
Answer: 15x4 cos 3x5
3. y = sin4 2x
Steps:
a. Write the dy/dx first.
b. Factor out.
c. Use the specific derivative formula.
d. Find the dy/dx.
Solution:
= y = sin4 2x
= Formula: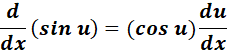
= 
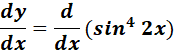
= x = sin4; dx = 4 sin3
= 
= 
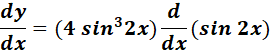
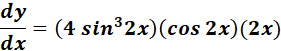
= 8 sin3 2x cos 2x
Answer: 8 sin3 2x cos 2x
4. 
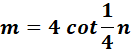
Steps:
a. Write the dm/dn first.
b. Use the specific derivative formula.
c. Find the dm/dn.
Solution:
=
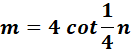
= Formula: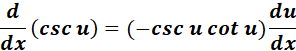
= 
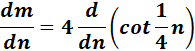
= n = 1/4 n; dn = 1/4
= 
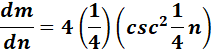
Answer: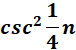 
5. c = tan n - n
Steps:
a. Write the dc/dn first.
b. Use the specific derivative formula.
c. Find the dc/dn.
d. Use the specific trigonometric identities.
Solution:
= c = tan n - n
= Formula: ;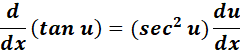 
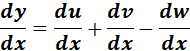
= Trigonometric Identity: tan = sec n - 1
= 
= 
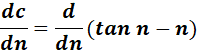
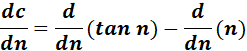
= n = tan n; dn = sec2 n
= 
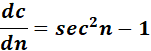
= tan2 n
Answer: tan2 n