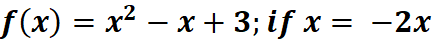
# 1st: Define the function
def f(x):  
    return x**2 - x + 3  # Define the function f(x) = x^2 - x + 3

# 2nd: Set the value of x
x = -2  # Assign the value -2 to x

# 3rd: Evaluate the function at x = -2
result = f(x)  # Evaluate f(x) and store the result in 'result'

# 4th: Print the result
print("f(x) =", result)  # Output the result of the function evaluation

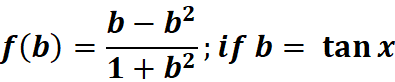
# 1st: Import the math module
import math  # Import math for trigonometric functions

# 2nd: Define the function
def f(b):  
    return (b - b**2) / (1 + b**2)  # Define the function f(b) = (b - b^2) / (1 + b^2)

# 3rd: Set the value of x and calculate b
x = 0.5  # Example value for x in radians
b = math.tan(x)  # Calculate b as tan(x)

# 4th: Evaluate the function at b = tan(x)
result = f(b)  # Evaluate f(b) and store the result in 'result'

# 5th: Print the result
print("f(b) =", result)  # Output the result of the function evaluation

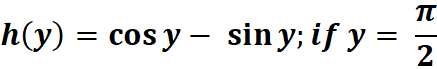
# 1st: Import the math module
import math  # Import math to access trigonometric functions and pi

# 2nd: Define the function
def h(y):  
    return math.cos(y) - math.sin(y)  # Define the function h(y) = cos(y) - sin(y)

# 3rd: Set the value of y and evaluate the function at y = pi/2
y = math.pi / 2  # Set y to pi/2 (90 degrees in radians)
result = h(y)  # Evaluate h(y) and store the result in 'result'

# 4th: Print the result
print("h(y) =", result)  # Output the result of the function evaluation

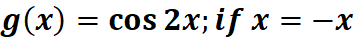
# 1st: Import the math module
import math  # Import math for trigonometric functions

# 2nd: Define the function
def g(x):  
    return math.cos(2 * x)  # Compute the cosine of 2x

# 3rd: Set the value of x and evaluate the function at x = 0
x = 0  # Set x to 0
result = g(x)  # Call the function g(x) with x = 0 and store the result

# 4th: Print the result
print(result)  # Output the result of g(0)

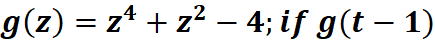
# 1st: Import the sympy module
import sympy as sp  # Import sympy for symbolic mathematics

# 2nd: Define the symbolic variable
t = sp.symbols('t')  # Define 't' as a symbolic variable

# 3rd: Define the expression for g(z)
z = t - 1  # Define z as t - 1
g_z = z**4 + z**2 - 4  # Define the expression g(z) = z^4 + z^2 - 4

# 4th: Substitute z = (t - 1) into g(z)
g_t_minus_1 = g_z.subs(z, t - 1)  # Substitute t - 1 for z in g(z)

# 5th: Expand the expression for g(t-1)
g_t_minus_1_expanded = sp.expand(g_t_minus_1)  # Expand the expression

# 6th: Print the expanded expression
print("Expanded expression for g(t-1):", g_t_minus_1_expanded)  # Output the result