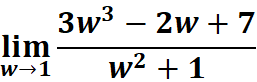
# 1st: Import necessary functions from sympy
from sympy import symbols, limit

# 2nd: Define the symbolic variable and expression
w = symbols('w')  # Declare 'w' as a symbolic variable
expression = (3*w**3 - 2*w + 7) / (w**2 + 1)  # Define the function to calculate the limit

# 3rd: Calculate the limit as w approaches 1
lim_result = limit(expression, w, 1)  # Compute the limit of the expression as w -> 1

# 4th: Output the result using custom print for LaTeX rendering
print(lim_result)  # Print the result of the limit calculation

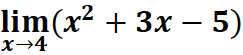
# 1st: Import necessary functions from sympy
from sympy import symbols, limit

# 2nd: Define the symbolic variable and function
x = symbols('x')  # Declare 'x' as a symbolic variable
f = x**2 + 3*x - 5  # Define the function f(x) = x² + 3x - 5

# 3rd: Calculate the limit as x approaches 4
lim_result = limit(f, x, 4)  # Compute the limit of f(x) as x → 4

# 4th: Output the result
print(lim_result)  # Print the computed limit result

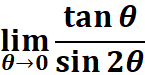
# 1st: Import necessary functions from sympy
from sympy import symbols, limit, tan, sin

# 2nd: Define the symbolic variable and mathematical expression
theta = symbols('theta')  # Declare 'theta' as a symbolic variable
expression = tan(theta) / sin(2 * theta)  # Define the function tan(θ) / sin(2θ)

# 3rd: Compute the limit as theta approaches 0
lim_result = limit(expression, theta, 0)  # Evaluate lim(θ→0) [tan(θ) / sin(2θ)]

# 4th: Display the computed result
print(lim_result)  # Output the calculated limit value

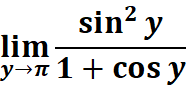
# 1st: Import necessary functions from sympy
from sympy import symbols, limit, exp

# 2nd: Define the variable and the function
z = symbols('z')  # Declare 'z' as a symbolic variable
expression = (exp(z) - 1) / z  # Define the function (e^z - 1) / z

# 3rd: Compute the limit as z approaches 0
lim_result = limit(expression, z, 0)  # Evaluate lim(z→0) [(e^z - 1) / z]

# 4th: Display the computed result
print(lim_result)  # Output the calculated limit value

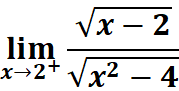
# 1st: Import necessary functions from sympy
from sympy import symbols, sqrt, limit

# 2nd: Define the variable and the function
x = symbols('x')  # Define 'x' as a symbolic variable
f = sqrt(x - 2) / sqrt(x**2 - 4)  # Define the function f(x) = sqrt(x - 2) / sqrt(x^2 - 4)

# 3rd: Calculate the limit as x approaches 2 from the right
lim_result = limit(f, x, 2, dir='+')  # Compute the limit of f(x) as x -> 2 from the right

# 4th: Print the result
print(lim_result)  # Output the result of the limit