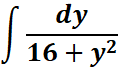
# 1st: Import the sympy module
import sympy as sp  # Import sympy for symbolic mathematics

# 2nd: Define the variable 'y'
y = sp.symbols('y')  # Define the symbolic variable 'y'

# 3rd: Define the integrand
integrand = 1 / (16 + y**2)  # Define the function to integrate

# 4th: Perform the integration with respect to 'y'
integral_result = sp.integrate(integrand, y)  # Compute the integral

# 5th: Display the result
sp.pprint(integral_result)  # Pretty print the result

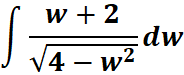
# 1st: Import the sympy module
import sympy as sp  # Import sympy for symbolic mathematics

# 2nd: Define the variable 'w'
w = sp.symbols('w')  # Define the symbolic variable 'w'

# 3rd: Define the integrand
integrand = (w + 2) / sp.sqrt(4 - w**2)  # Define the function to integrate

# 4th: Perform the integration with respect to 'w'
integral_result = sp.integrate(integrand, w)  # Compute the integral

# 5th: Display the result
sp.pprint(integral_result)  # Pretty print the result

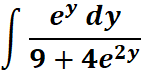
# 1st: Import the sympy module
import sympy as sp  # Import sympy for symbolic mathematics

# 2nd: Define the variable 'y'
y = sp.symbols('y')  # Define the symbolic variable 'y'

# 3rd: Define the integrand
integrand = sp.exp(y) / (9 + 4 * sp.exp(2 * y))  # Define the function to integrate

# 4th: Perform the integration with respect to 'y'
integral_result = sp.integrate(integrand, y)  # Compute the integral

# 5th: Display the result
sp.pprint(integral_result)  # Pretty print the result

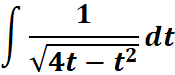
# 1st: Import the sympy module
import sympy as sp  # Import sympy for symbolic mathematics

# 2nd: Define the variable 't'
t = sp.symbols('t')  # Define the symbolic variable 't'

# 3rd: Define the integrand
integrand = 1 / sp.sqrt(4 * t - t**2)  # Define the function to integrate

# 4th: Perform the integration with respect to 't'
integral_result = sp.integrate(integrand, t)  # Compute the integral

# 5th: Display the result
sp.pprint(integral_result)  # Pretty print the result

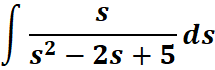
# 1st: Import the sympy module
import sympy as sp  # Import sympy for symbolic mathematics

# 2nd: Define the variable 's'
s = sp.symbols('s')  # Define the symbolic variable 's'

# 3rd: Define the integrand
integrand = s / (s**2 - 2*s + 5)  # Define the function to integrate

# 4th: Perform the integration with respect to 's'
integral_result = sp.integrate(integrand, s)  # Compute the integral

# 5th: Display the result
sp.pprint(integral_result)  # Pretty print the result