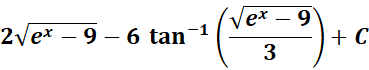Definition
Algebraic Substitution
-> a technique that simplify an integral by making a substitution. This involves replacing a complicated part of the integrand (the function being integrated) with a new variable to make the integral easier to solve.
Steps to use Algebraic Substitution |
1. Identify a part of the integrand.
2. Choose a substitution.
3. Find the derivative ??/?? or rewrite ?? = g′(x) dx.
4. Substitute the new variable ? into the integral.
5. Solve the integral in terms of ?.
6. Back - substitute the original variable ?.
Example |
1. Find the answer from this given:
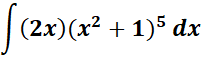
Steps:
1. Choose the integrand.
2. Choose the substitution.
3. Use derivative.
4. Substitute the new u into integral.
5. Find the algebraic solution.
=
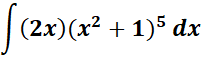
= u = x2 + 1; du = 2x dx
= Substitute: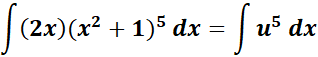 
= Formula: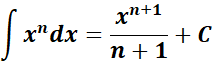 
= 
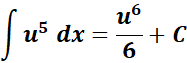
= Use Back - substitution:
= 
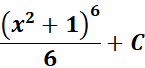
Exercise |
1. 
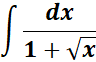
Steps:
a. Choose the integrand.
b. Choose the substitution.
c. Use derivative.
d. Substitute the new u into integral.
e. Find the algebraic solution.
Solution:
=
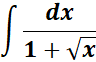
= Formula: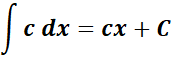 
; 
= u = 
; x = u2; dx = 2u du
= Substitute: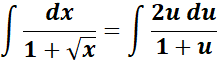 
= 
= 
= 
= 
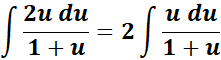
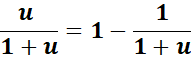
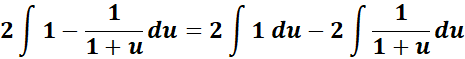
= Use Back - substitution:
= 
Answer:
2. 
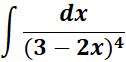
Steps:
a. Choose the integrand.
b. Choose the substitution.
c. Use derivative.
d. Substitute the new u into integral.
e. Find the algebraic solution.
Solution:
=
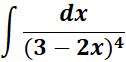
= Formula: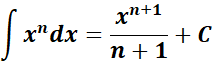
= u = 3 - 2x; du = -2 dx; dx = - du/2
= Substitute: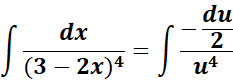 
= 
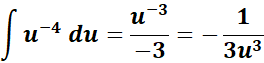
= Multiply: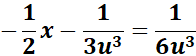 
= Use Back - substitution:
= 
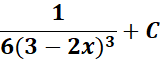
Answer: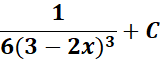
3. 
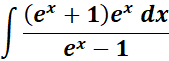
Steps:
a. Choose the integrand.
b. Choose the substitution.
c. Use derivative.
d. Substitute the new u into integral.
e. Find the algebraic solution.
Solution:
=
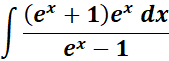
= Rewrite: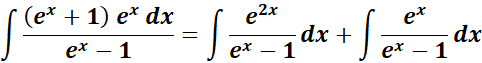 
= 1st term: u = ex - 1; du = ex dx
= 
= 
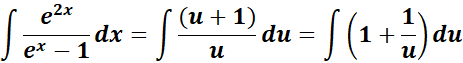
= 2nd integral: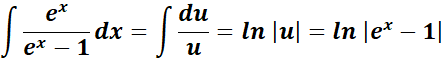 
= Combine:
= 
= 
Answer:
4. 
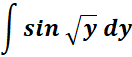
Steps:
a. Choose the integrand.
b. Choose the substitution.
c. Use derivative.
d. Substitute the new u into integral.
e. Find the algebraic solution.
Solution:
=
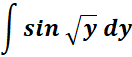
= Formula: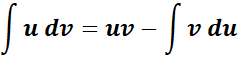 
; 
= 
= 
= 
= 
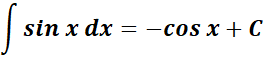
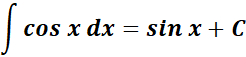
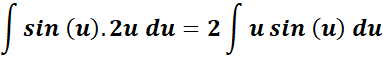
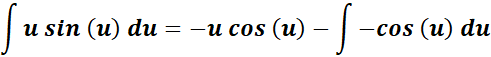
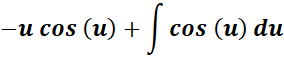
= Integrate: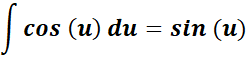 
= 
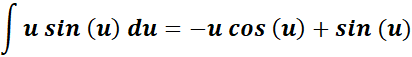
= Use Back - substitution:
= 
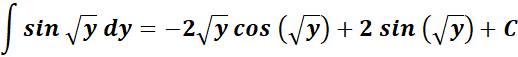
Answer: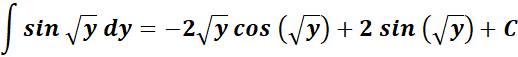
5. 
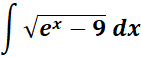
Steps:
a. Choose the integrand.
b. Choose the substitution.
c. Use derivative.
d. Substitute the new u into integral.
e. Find the algebraic solution.
Solution:
=
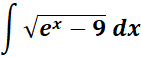
= Formula: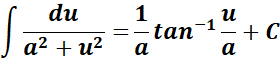 
= u = ex - 9; du = ex dx; dx = du/u + 9
= Substitute: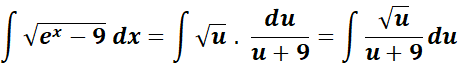 
= 
= 
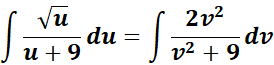
= Integrate: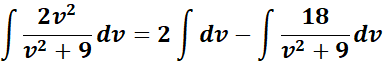 
= 
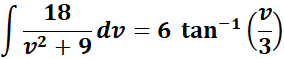
= Combine: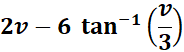 
= Use Back - substitution:
= 
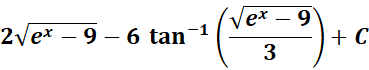
Answer: