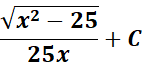Definition
Trigonometric Substitution
-> a technique that simplify integrals involving square roots of quadratic expressions. This method leverages trigonometric identities to transform a complex integral into a simpler form that can be more easily evaluated.
Steps to use Trigonometric Substitution |
1. Identify the form of the integral.
2. Choose the appropriate substitution.
3. Compute the differential form.
4. Substitute into the Integral and simplify.
5. Back - Substitute
Integral and Substitution Forms: |
1. 
2. 
3. 
4. 
5. 
6. 
Example |
1. Find the answer from this given:
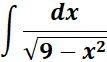
Steps:
1. Identify the integral form.
2. Choose the trigonometric substitution.
3. Use the derivative.
4. Substitute to integral and simplify.
5. Use back - substitute and find the trigonometric solution.
=
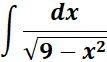
= a2 = 9; a = 3
= Formula:
= 
; 
; 
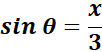
= Substitute: 
= 
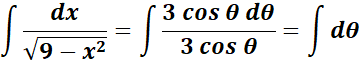
= Integrate: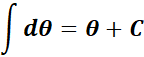 
= Use Back - Substitution:
= 
= 
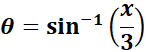
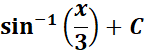
Exercises |
1. 
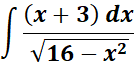
Steps:
a. Identify the integral form.
b. Choose the trigonometric substitution.
c. Use the derivative.
d. Substitute to integral and simplify.
e. Use back - substitute and find the trigonometric solution.
Solution:
=
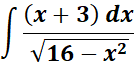
= Formula:
= a2 = 16; a = 4
= 
; 
; 
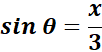
= Substitute: 
= 
= 
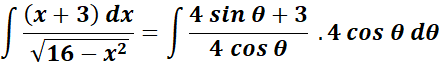
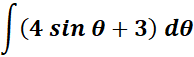
= Integrate: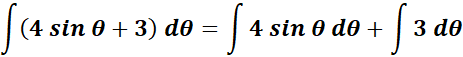 
= 
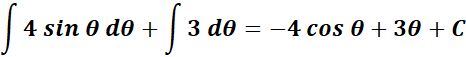
= Use Back - Substitution:
= 
; 
= 
= 
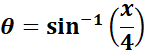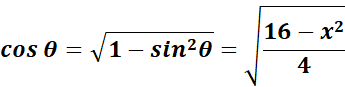
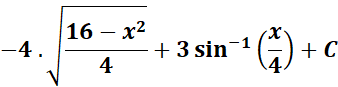
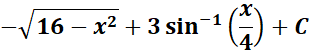
Answer: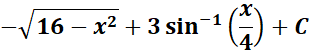
2. 
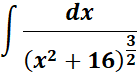
Steps:
a. Identify the integral form.
b. Choose the trigonometric substitution.
c. Use the derivative.
d. Substitute to integral and simplify.
e. Use back - substitute and find the trigonometric solution.
Solution:
=
=
= 
; 
; 
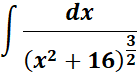
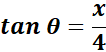
= Substitute: 
= Use identity: 
= 
= 
= 
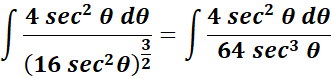
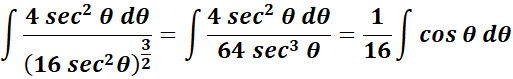
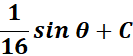
= Use Back - Substitute:
= 
= 
= 
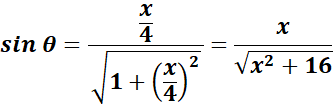
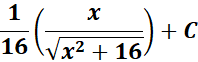
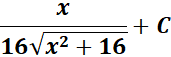
Answer: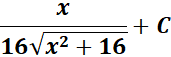
3. 
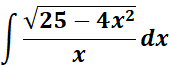
Steps:
a. Identify the integral form.
b. Choose the trigonometric substitution.
c. Use the derivative.
d. Substitute to integral and simplify.
e. Use back - substitute and find the trigonometric solution.
Solution:
=
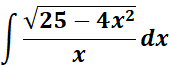
= Formula:
= a2 = 25; a = 5
= 
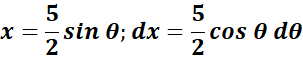
= Substitute: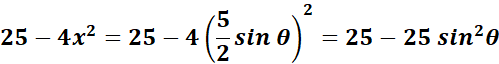 
= Use Identity: 
= 
= 
= 
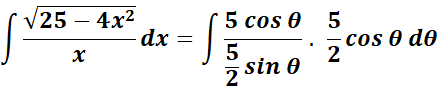
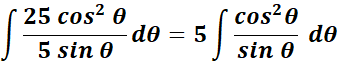
= Integrate: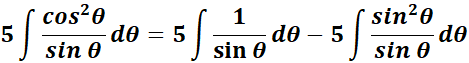 
= 
= 
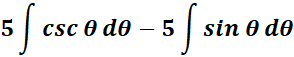
= Use Back - Substitute:
= 
= 
; 
= 
= 
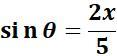
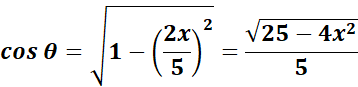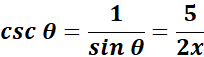
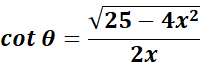
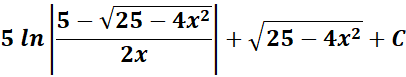
Answer: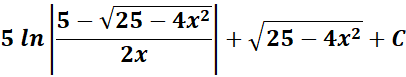
4. 
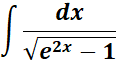
Steps:
a. Identify the integral form.
b. Choose the trigonometric substitution.
c. Use the derivative.
d. Substitute to integral and simplify.
e. Use back - substitute and find the trigonometric solution.
Solution:
=
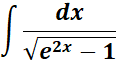
= u = ex; dx = du/u; e2x = u2
= 
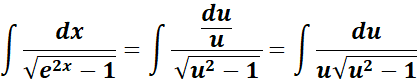
= Use Back - Substitute:
= 
= 
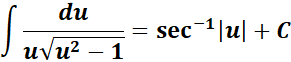
Answer:
5. 
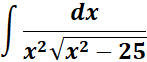
Steps:
a. Identify the integral form.
b. Choose the trigonometric substitution.
c. Use the derivative.
d. Substitute to integral and simplify.
e. Use back - substitute and find the trigonometric solution.
Solution:
=
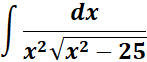
= Formula:
= 
; 
= 
= 
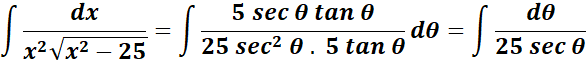
= Integrate: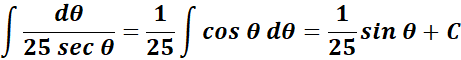 
= Use Back - Substitution:
= 
= 
= 
= 
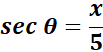
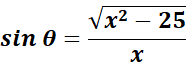
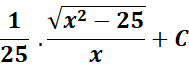
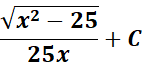
Answer: