Definition
Integration by Parts
-> a technique that uses to integrate products of functions.
Symbol:
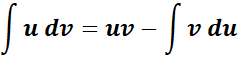
Where:
u and v - differentiable functions of ?.
du - derivative of ? and ?? is the differential of ?.
Steps to use By Parts Formula |
1. Select u and dv.
2. Differentiate u and integrate dv.
3. Apply the by parts formula.
Example |
1. Find the answer from this given:
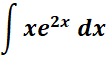
Steps:
1. Choose the u and dv.
2. Differentiate the u and dv must be integrate.
3. Apply the integration by parts.
=
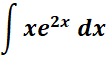
= u = x; du = dx;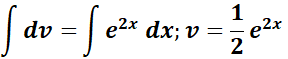 
= 
= 
= 
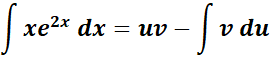
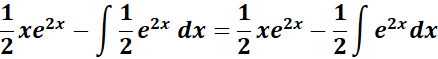
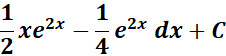
Exercises |
1. 
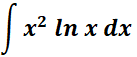
Steps:
a. Choose the u and dv.
b. Differentiate the u and dv must be integrate.
c. Apply the integration by parts.
Solution:
=
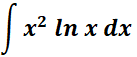
= u = ln x; du = dx/x; v =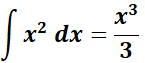 
= 
= 
= 
= 
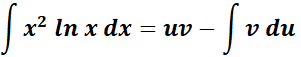
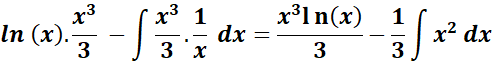
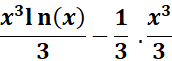
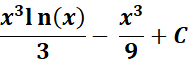
Answer: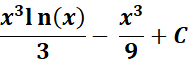
2. 
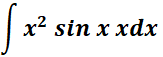
Steps:
a. Choose the u and dv.
b. Differentiate the u and dv must be integrate.
c. Apply the integration by parts.
Solution:
=
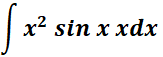
= u = x2; du = 2x dx;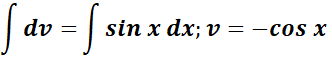 
= 
= 
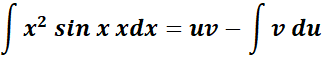
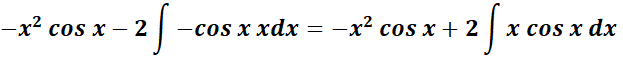
= Integrate the second part: u = x; du = dx;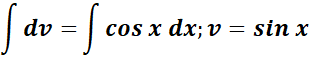 
= 
= 
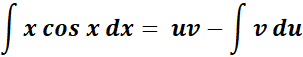
= Combine: 
= 
Answer:
3. 
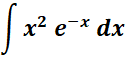
Steps:
a. Choose the u and dv.
b. Differentiate the u and dv must be integrate.
c. Apply the integration by parts.
Solution:
=
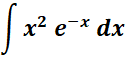
= u = x2; du = 2x dx;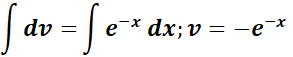 
= 
= 
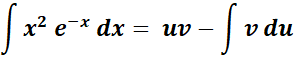
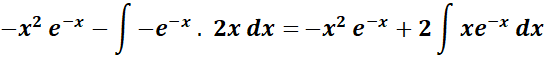
= Integrate the second part: u = x; du = dx;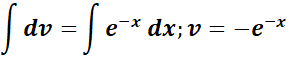 
= 
= 
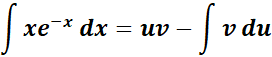
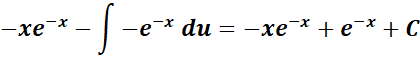
= Combine: 
= 
Answer:
4. 
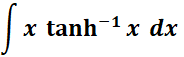
Steps:
a. Choose the u and dv.
b. Differentiate the u and dv must be integrate.
c. Apply the integration by parts.
Solution:
=
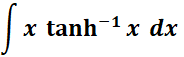
= u = tanh-1 x; du = dx/1 - x2;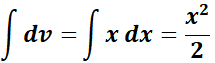 
= 
= 
= 
= 
= 
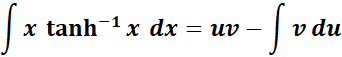
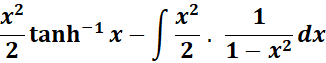
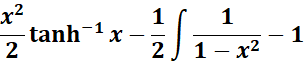
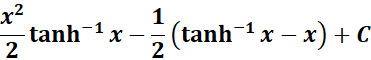
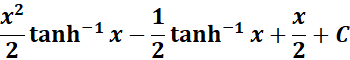
Answer: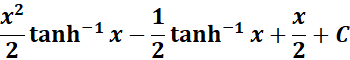
5. 
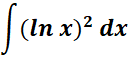
Steps:
a. Choose the u and dv.
b. Differentiate the u and dv must be integrate.
c. Apply the integration by parts.
Solution:
=
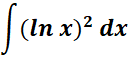
= u = (ln x)2; du = 2 ln x dx/x;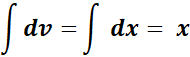 
= 
= 
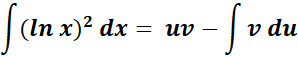
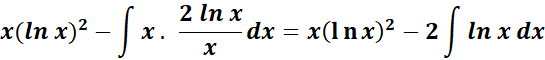
= Integrate the second part: u = ln x; du = dx/x;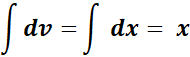
= 
= 
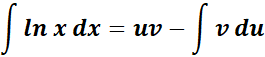
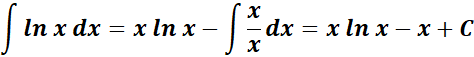
= Combine: 
= 
Answer: