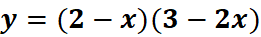
# 1st: Import the sympy module
import sympy as sp # Import SymPy for symbolic mathematics

# 2nd: Define the symbolic variable
x = sp.symbols('x') # Define 'x' as a symbolic variable

# 3rd: Define the function y
y = (2 - x) * (3 - 2 * x) # Define the function y = (2 - x)(3 - 2x)

# 4th: Define y + delta y by replacing x with x + delta x in the original equation
delta_x = sp.symbols('delta_x')  # Define delta_x as a symbolic variable
y_plus_delta_y = (2 - (x + delta_x)) * (3 - 2 * (x + delta_x)) # Replace x with x + delta_x

# 5th: Subtract the original function y from y + delta y
difference = y_plus_delta_y - y  # Subtract the original function

# 6th: Divide both sides by delta_x
difference_over_delta_x = difference / delta_x  # Divide by delta_x

# 7th: Find the limit as delta_x approaches 0
derivative = sp.limit(difference_over_delta_x, delta_x, 0) # Take the limit as delta_x -> 0

# 8th: Display the original function and its derivative
print("Original Function (y):")
sp.pprint(y, use_unicode=True) # Pretty print the original function y

print("\nDerivative of y with respect to x:")
sp.pprint(derivative, use_unicode=True) # Pretty print the derivative of y

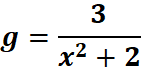
# 1st: Import the sympy module
import sympy as sp # Import SymPy for symbolic mathematics

# 2nd: Define the symbolic variable
x = sp.symbols('x') # Define 'x' as a symbolic variable

# 3rd: Define the function g
g = 3 / (x**2 + 2) # Define the function g = 3 / (x^2 + 2)

# 4th: Define g + delta g by replacing x with x + delta x in the original equation
delta_x = sp.symbols('delta_x')  # Define delta_x as a symbolic variable
g_plus_delta_g = 3 / ((x + delta_x)**2 + 2) # Replace x with x + delta_x

# 5th: Subtract the original function g from g + delta g
difference = g_plus_delta_g - g # Subtract the original function

# 6th: Divide both sides by delta_x
difference_over_delta_x = difference / delta_x # Divide by delta_x

# 7th: Find the limit as delta_x approaches 0
derivative = sp.limit(difference_over_delta_x, delta_x, 0) # Take the limit as delta_x -> 0

# 8th: Display the original function and its derivative
print("Original Function (g):")
sp.pprint(g, use_unicode=True) # Pretty print the original function g

print("\nDerivative of g with respect to x:")
sp.pprint(derivative, use_unicode=True) # Pretty print the derivative of g

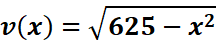
# 1st: Import the sympy module
import sympy as sp # Import SymPy for symbolic mathematics

# 2nd: Define the symbolic variable
x = sp.symbols('x') # Define 'x' as a symbolic variable

# 3rd: Define the function v(x)
v = sp.sqrt(625 - x**2) # Define the function v(x) = sqrt(625 - x^2)

# 4th: Define v + delta v by replacing x with x + delta x in the original equation
delta_x = sp.symbols('delta_x') # Define delta_x as a symbolic variable
v_plus_delta_v = sp.sqrt(625 - (x + delta_x)**2) # Replace x with x + delta_x

# 5th: Subtract the original function v(x) from v + delta v
difference = v_plus_delta_v - v # Subtract the original function

# 6th: Divide both sides by delta_x
difference_over_delta_x = difference / delta_x # Divide by delta_x

# 7th: Find the limit as delta_x approaches 0
derivative = sp.limit(difference_over_delta_x, delta_x, 0) # Take the limit as delta_x -> 0

# 8th: Display the original function and its derivative
print("Original Function v(x):")
sp.pprint(v, use_unicode=True) # Pretty print the original function v(x)

print("\nDerivative of v(x) with respect to x:")
sp.pprint(derivative, use_unicode=True) # Pretty print the derivative of v(x)

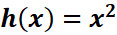
# 1st: Import the sympy module
import sympy as sp # Import SymPy for symbolic mathematics

# 2nd: Define the symbolic variable
x = sp.symbols('x') # Define 'x' as a symbolic variable

# 3rd: Define the function h(x)
h = x**2 # Define the function h(x) = x^2

# 4th: Define h + delta h by replacing x with x + delta x in the original equation
delta_x = sp.symbols('delta_x') # Define delta_x as a symbolic variable
h_plus_delta_h = (x + delta_x)**2 # Replace x with x + delta_x

# 5th: Subtract the original function h(x) from h + delta h
difference = h_plus_delta_h - h # Subtract the original function

# 6th: Divide both sides by delta_x
difference_over_delta_x = difference / delta_x # Divide by delta_x

# 7th: Find the limit as delta_x approaches 0
derivative = sp.limit(difference_over_delta_x, delta_x, 0) # Take the limit as delta_x -> 0

# 8th: Display the original function and its derivative
print("Original Function h(x):")
sp.pprint(h, use_unicode=True) # Pretty print the original function h(x)

print("\nDerivative of h(x) with respect to x:")
sp.pprint(derivative, use_unicode=True) # Pretty print the derivative of h(x)

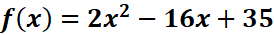
# 1st: Import the sympy module
import sympy as sp # Import SymPy for symbolic mathematics

# 2nd: Define the symbolic variable
x = sp.symbols('x') # Define 'x' as a symbolic variable

# 3rd: Define the function f(x)
f = 2*x**2 - 16*x + 35 # Define the function f(x) = 2x^2 - 16x + 35

# 4th: Define f + delta f by replacing x with x + delta x in the original equation
delta_x = sp.symbols('delta_x') # Define delta_x as a symbolic variable
f_plus_delta_f = 2*(x + delta_x)**2 - 16*(x + delta_x) + 35 # Replace x with x + delta_x

# 5th: Subtract the original function f(x) from f + delta f
difference = f_plus_delta_f - f # Subtract the original function

# 6th: Divide both sides by delta_x
difference_over_delta_x = difference / delta_x # Divide by delta_x

# 7th: Find the limit as delta_x approaches 0
derivative = sp.limit(difference_over_delta_x, delta_x, 0) # Take the limit as delta_x -> 0

# 8th: Display the original function and its derivative
print("Original Function f(x):")
sp.pprint(f, use_unicode=True) # Pretty print the original function f(x)

print("\nDerivative of f(x) with respect to x:")
sp.pprint(derivative, use_unicode=True) # Pretty print the derivative of f(x)