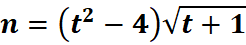
# 1st: Import the sympy module  
import sympy as sp  # Import SymPy for symbolic mathematics  

# 2nd: Define the symbolic variable  
t = sp.symbols('t')  # Define 't' as a symbolic variable  

# 3rd: Define the function n(t)  
n = (t**2 - 4) * sp.sqrt(t + 1)  # Define the function n(t) = (t² - 4) * √(t + 1)  

# 4th: Compute the derivative of n(t) with respect to t  
n_derivative = sp.diff(n, t)  

# 5th: Display the original function and its derivative using pretty printing  
print("Function n(t):")  
sp.pprint(n, use_unicode=True)  # Pretty print the function  

print("\nDerivative of n(t):")  
sp.pprint(n_derivative, use_unicode=True)  # Pretty print the derivative  

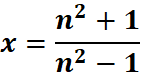
# 1st: Import the sympy module  
import sympy as sp  # Import SymPy for symbolic mathematics  

# 2nd: Define the symbolic variable  
n = sp.symbols('n')  # Define 'n' as a symbolic variable  

# 3rd: Define the function x(n)  
x = (n**2 + 1) / (n**2 - 1)  # Define the function x(n) = (n² + 1) / (n² - 1)  

# 4th: Compute the derivative of x(n) with respect to n  
x_derivative = sp.diff(x, n)  

# 5th: Display the original function and its derivative using pretty printing  
print("Function x(n):")  
sp.pprint(x, use_unicode=True)  # Pretty print the function  

print("\nDerivative of x(n):")  
sp.pprint(x_derivative, use_unicode=True)  # Pretty print the derivative  

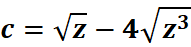
# 1st: Import the sympy module  
import sympy as sp  # Import SymPy for symbolic mathematics  

# 2nd: Define the symbolic variable  
z = sp.symbols('z')  # Define 'z' as a symbolic variable  

# 3rd: Define the function c(z)  
c = sp.sqrt(z) - 4 * sp.sqrt(z**3)  # Define c(z) = sqrt(z) - 4 * sqrt(z³)  

# 4th: Compute the derivative of c(z) with respect to z  
c_derivative = sp.diff(c, z)  

# 5th: Display the original function and its derivative using pretty printing  
print("Function c(z):")  
sp.pprint(c, use_unicode=True)  # Pretty print the function  

print("\nDerivative of c(z):")  
sp.pprint(c_derivative, use_unicode=True)  # Pretty print the derivative  

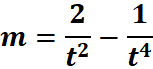
# 1st: Import the sympy module  
import sympy as sp  # Import SymPy for symbolic mathematics  

# 2nd: Define the symbolic variable  
t = sp.symbols('t')  # Define 't' as a symbolic variable  

# 3rd: Define the function m(t)  
m = (2 / t**2) - (1 / t**4)  # Define m(t) = (2/t²) - (1/t⁴)  

# 4th: Compute the derivative of m(t) with respect to t  
m_derivative = sp.diff(m, t)  

# 5th: Display the original function and its derivative using pretty printing  
print("Function m(t):")  
sp.pprint(m, use_unicode=True)  # Pretty print the function  

print("\nDerivative of m(t):")  
sp.pprint(m_derivative, use_unicode=True)  # Pretty print the derivative  

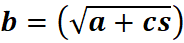
# 1st: Import the sympy module  
import sympy as sp  # Import SymPy for symbolic mathematics  

# 2nd: Define the symbolic variables  
a, c, s = sp.symbols('a c s')  # Define 'a', 'c', and 's' as symbolic variables  

# 3rd: Define the function b(a, c, s)  
b = sp.sqrt(a + c * s)  # Define b = sqrt(a + c*s)  

# 4th: Compute the derivative of b with respect to a  
b_derivative = sp.diff(b, a)  

# 5th: Display the original function and its derivative using pretty printing  
print("Function b(a, c, s):")  
sp.pprint(b, use_unicode=True)  # Pretty print the function  

print("\nDerivative of b with respect to a:")  
sp.pprint(b_derivative, use_unicode=True)  # Pretty print the derivative