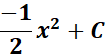Formulas of Integral - II
1. Using Chain Rule in Integration
-> also known as u - Substitution, where it deals with a composite function, it must simplify the integral by substituting a part of the integral (usually the inner function) with a new variable, and simplify.
Formula:
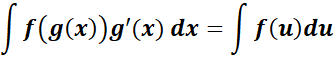
2. Implicit Differentiation in Integration
-> it involves finding an antiderivative when the function is not explicitly solved for one variable.
Formula:
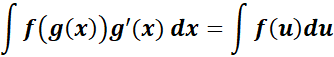
3. Parametric Equations in Integration
-> the integration with respect to the parameter. If ? and ? are given as functions of a parameter ?, find the integral with respect to ?.
Formula:
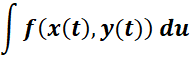
Example |
1. Find the answer from this given:
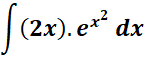
Steps:
a. Write the given 1st.
b. Use the specific integral formula.
c. Find the integral.
=
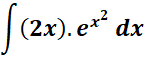
= u = x2; du = 2x dx
= 
= 
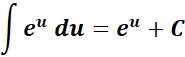
Exercises |
1. 
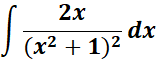
Steps:
a. Write the given 1st.
b. Use the specific integral formula.
c. Find the integral.
Solution:
=
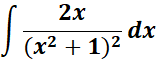
= Formula: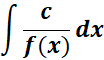 
= u = x2 + 1; du = 2x
= 
= 
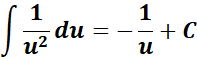
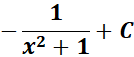
Answer: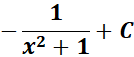
2. 
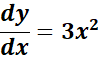
Steps:
a. Write the given 1st.
b. Use the specific integral formula.
c. Find the integral.
Solution:
=
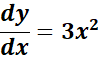
= Formula: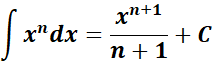 
= 
= 
= 
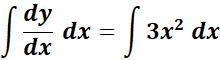
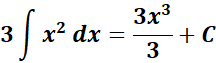
Answer:
3. 
Steps:
a. Write the given 1st.
b. Use the specific integral formula.
c. Find the integral.
Solution:
=
= Formula: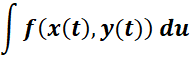
= x = t2 + 1; dx = 2t
= 
= 
= 
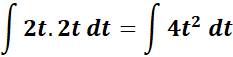
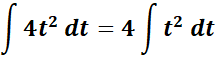
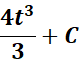
Answer: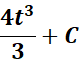
4. 
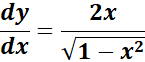
Steps:
a. Write the given 1st.
b. Use the specific integral formula.
c. Find the integral.
Solution:
=
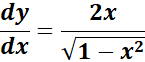
= Formula: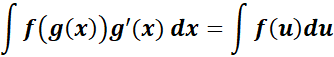
= 
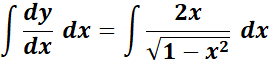
= u = 1 - x2; du = -2x dx
= Use this for substitution: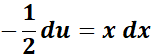 
= 
= 
= 
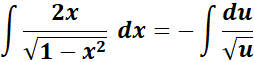
Answer:
5. 
Steps:
a. Write the given 1st.
b. Use the specific integral formula.
c. Find the integral.
Solution:
=
= Formula: ;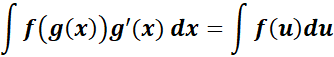 
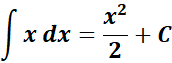
= u = x2; du = 2x; v = y2 = dv = 2y
= 
= 
= 
= 
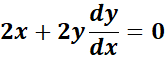
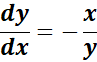
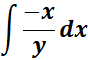
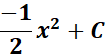
Answer: