Definition
Definite Integral
-> also known as Riemann Integral that the bound to lie on the real line.
Symbol:
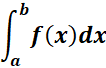
Where:
It contains the upper (b) and lower (a) limits.
X where is restricted to lie on a real line.
Properties of Definite Integral |
1. Linearity Rule
-> the c1 and c2 are constants.
Formula:
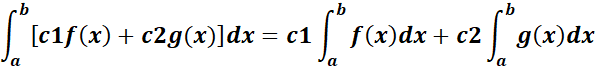
2. Additivity (Internal Addition) Rule
-> a < c < b.
Formula:
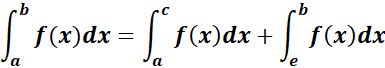
3. Limit Reversal Rule
-> switching the limits changes the sign of the integral.
Formula:
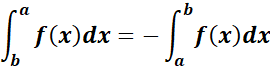
4. Zero Width Interval Rule
-> the integral over an interval of 0 width is 0.
Formula:
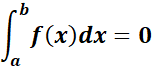
5. Fundamental Theorem of Calculus Rule - 1
-> the F(x) is an antiderivative of f(x) on [a,b].
Formula:
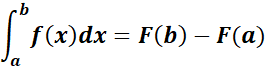
6. Fundamental Theorem of Calculus Rule - 2
-> the F(x)
Formula:
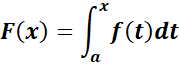
Example |
1. Find the answer from this given:
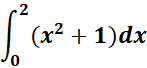
Steps:
a. Write the given 1st.
b. Use the specific indefinite properties formula.
c. Use the specific definite properties formula.
d. Find the definite integral.
=
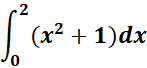
= C = 1; n = 2; n +1 = 3
= 
= 
; 
= 
= 
= 
; 
= 
= 
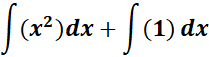
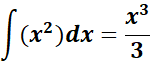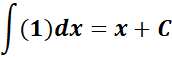
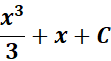
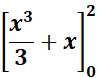
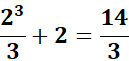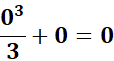
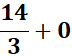
Exercises |
1. 
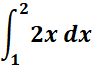
Steps:
a. Write the given 1st.
b. Use the specific indefinite properties formula.
c. Use the specific definite properties formula.
d. Find the definite integral.
Solution:
=
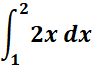
= Formula: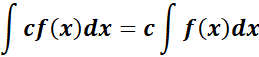 
; 
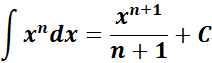
= c = 1; n = 1; n + 1 = 2
= 
; 
= 
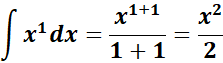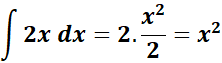
= (22) - (12) = 4 - 1
= 3
Answer: 3
2. 
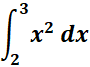
Steps:
a. Write the given 1st.
b. Use the specific indefinite properties formula.
c. Use the specific definite properties formula.
d. Find the definite integral.
Solution:
=
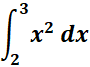
= Formula: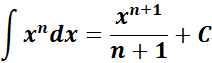
= n = 2; n + 1 = 3
= 
= 
= 
= 
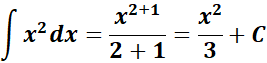
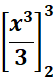
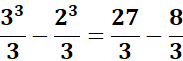
Answer:
3. 
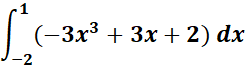
Steps:
a. Write the given 1st.
b. Use the specific indefinite properties formula.
c. Use the specific definite properties formula.
d. Find the definite integral.
Solution:
=
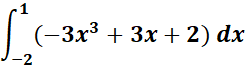
= Formula: ;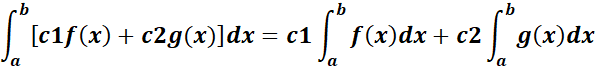
= ;
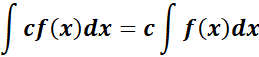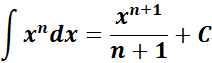
= c1 = -3; c2 = 3; c3 = 2; n1 = 3; n1 + 1 = 4; n2 = 1; n2 + 1 = 1
= 
= 
= 
= 
= 
; 
= 
= 
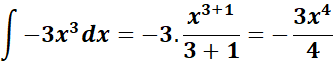
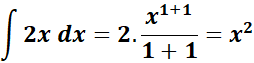
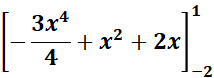
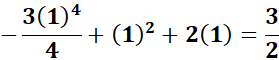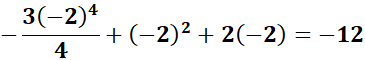
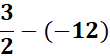
Answer:
4. 
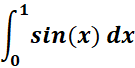
Steps:
a. Write the given 1st.
b. Use the specific indefinite properties formula.
c. Use the specific definite properties formula.
d. Find the definite integral.
Solution:
=
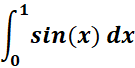
= Formula: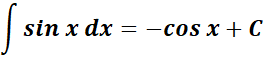 
= - cos (x) + C
= 
= - cos (1)
= - cos (0)
= - cos (1) - ( -cos (0) )
= 1 - cos (1)
Answer: 1 - cos (1)
5. 
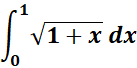
Steps:
a. Write the given 1st.
b. Use the specific indefinite properties formula.
c. Use the specific definite properties formula.
d. Find the definite integral.
Solution:
=
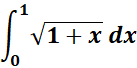
= Formula: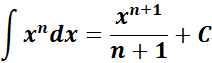
= c = 1; n = 1/2; n + 1 = 3/2
= 
= 
= 
= 
= 
;
= 
= 
= 
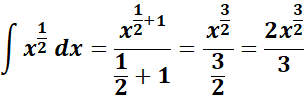
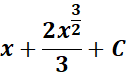
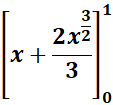
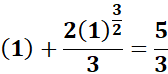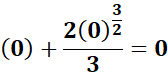
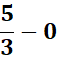
Answer: