Definition
Integral Calculus
-> the branch of mathematics where the study of integrals and along with properties.
Indefinite Integral
-> also as antiderivative, that is not using upper and lower limit.
Symbol:
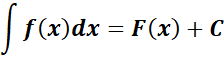
Where:
F(x) is anti - derivative or primitive.
f(x) is called the integrand.
dx is called integrating agent.
C is called integration constant.
x is called integration constant.
Properties of Indefinite Integral |
1. Linearity Rule
-> this is where the linear combination of functions is the integral of linear combinations.
Formula:
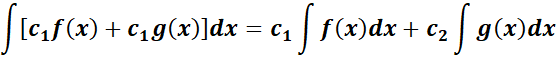
2. Constant Multiple Rule
-> this is where factor out constants from integrals.
Formula:
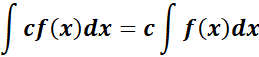
3. Power Rule
-> the integration of x powers and must n is not equal to 1.
Formula:
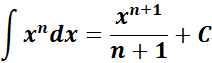
4. Sum Rule
-> the integration sum of two functions is the sum integrals.
Formula:
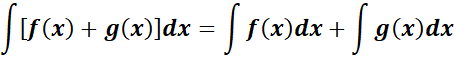
5. Difference Rule
-> the integration difference between two functions is the difference integrals.
Formula:
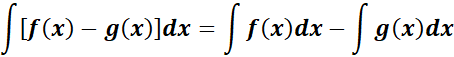
6. Zero Integral
-> the integration over an 0 interval width yields 0.
Formula:
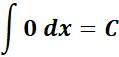
7. Integration by Substitution
-> the simplify of integrals by changing variables.
Formula:
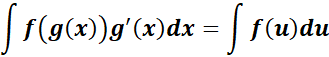
8. Integration by Parts
-> the integration products of functions.
Formula:
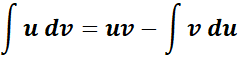
Example |
1. Find the answer from this given:
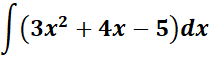
Steps:
a. Write the given 1st.
b. Use the specific indefinite properties formula.
c. Find the indefinite integral.
=
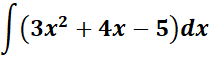
= c1 = 3; c2 = 4; c3 = -5
= n1 = 2; n1 +1 = 3; n2 = 1; n2 + 1 = 2
= 
= 
= 
; 
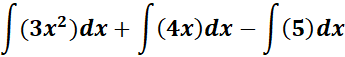
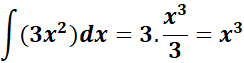
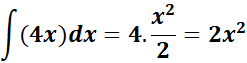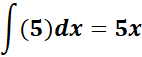
= x3 + 2x2 - 5x + C
Exercises |
1. 
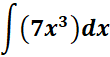
Steps:
a. Write the given 1st.
b. Use the specific indefinite properties formula.
c. Find the indefinite integral.
Solution:
=
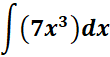
= Formula: ;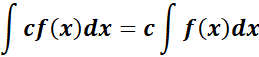
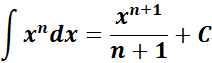
= c = 7; n = 3; n + 1 = 4
= 
= 
= 
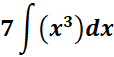
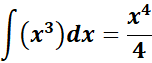
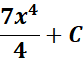
Answer: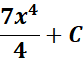
2. 
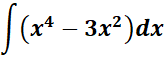
Steps:
a. Write the given 1st.
b. Use the specific indefinite properties formula.
c. Find the indefinite integral.
Solution:
=
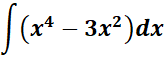
= Formula: ;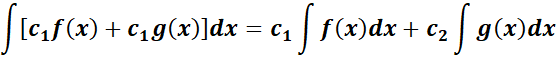
=
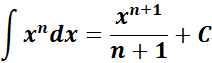
= c = -3; n1 = 4; n1 + 1 = 5;
= 
= 
; 
= 
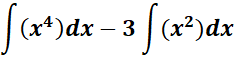
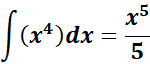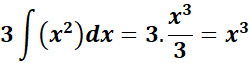
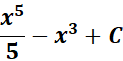
Answer: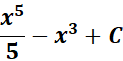
3. 
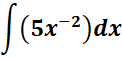
Steps:
a. Write the given 1st.
b. Use the specific indefinite properties formula.
c. Find the indefinite integral.
Solution:
=
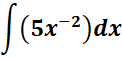
= Formula: ;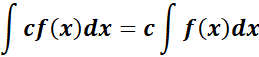
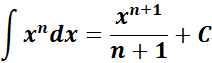
= c = 5; n = -2; n + 1 = -1
= 
= 
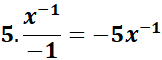
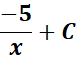
Answer: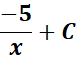
4. 
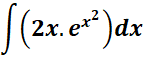
Steps:
a. Write the given 1st.
b. Use the specific indefinite properties formula.
c. Find the indefinite integral.
Solution:
=
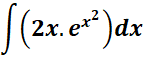
= Formula: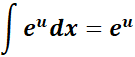 
= u = x2; du = 2x dx
= 
Answer:
5. 
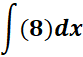
Steps:
a. Write the given 1st.
b. Use the specific indefinite properties formula.
c. Find the indefinite integral.
Solution:
=
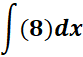
= Formula: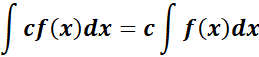
= c = 8
= 
= 
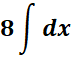
Answer: