| Non - Repeated Linear Factors |
Nov. 30, 2024, 6:13 p.m.
Definition
Rational Fraction
-> the rational fraction is the ratio of two polynomials.
Symbol:
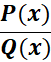
Where:
P(x) and Q(x) - polynomials, where Q(x) must not be equal to 0.
Partial Fraction
-> the rational fraction may be broken into a sum of simpler fractions.
Non - Repeated Linear Fraction
-> the denominator is a product of distinct linear factors.
Symbol:
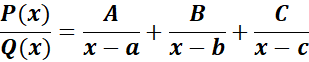
Where:
A, B, and C - constants to be determined.
Steps to use Linear Fraction |
1. Factor the denominator.
2. Setup the partial fraction for decomposition.
3. Multiply both sides by the denominator.
4. Expand and collect terms.
5. Solve the equation system.
6. Substitute the constants.
7. Integrate each terms and find the non - repeated linear fraction.
Example |
1. Find the answer from this given:
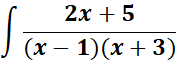
Steps:
1. The denominator must factored.
2. The partial fraction must be decomposition.
3. Use the denominator to multiply.
4. Expand, collect terms and solve the overall equation system.
5. Substitute the constants, integrate and find the non - repeated linear fraction.
= 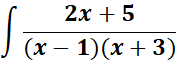
= A = (x - 1); B = (x + 3)
= 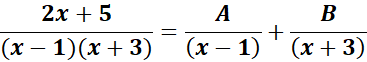
= ![]() ;
; ![]()
= ![]()
= Solve for A and B:
= x: A + B = 2
= Constant: 3A - B = 5
= 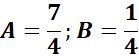
= 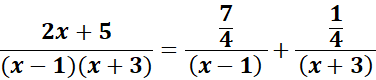
= Formula: 
= 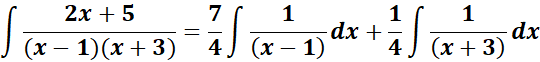
= 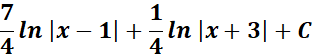
Exercises |
1. 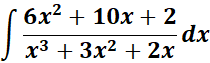
Steps:
a. The denominator must factored.
b. The partial fraction must be decomposition.
c. Use the denominator to multiply.
d. Expand, collect terms and solve the overall equation system.
e. Substitute the constants, integrate and find the non - repeated linear fraction.
Solution:
= 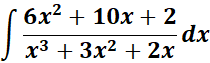
= Formula: 
= A = x; B = (x + 1); C = (x +2)
= 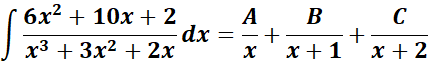
= ![]()
= ![]()
= Solve for A, B and C:
= x2: A + B + C = 6
= x: 3A + 2B + C = 10
= Constant: 2A = 2
= A = 1; B = 2; C = 3
= 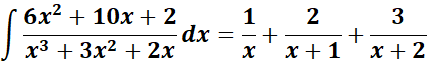
= 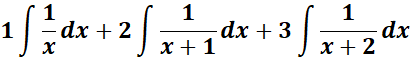
= ![]()
Answer: ![]()
2. 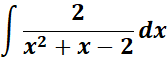
Steps:
a. The denominator must factored.
b. The partial fraction must be decomposition.
c. Use the denominator to multiply.
d. Expand, collect terms and solve the overall equation system.
e. Use log identity.
e. Substitute the constants, integrate and find the non - repeated linear fraction.
Solution:
= 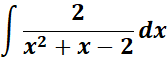
= Formula: 
= A = (x + 2); B = (x - 1)
= 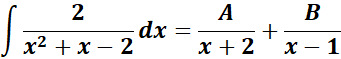
= ![]()
= ![]()
= Solve for A and B:
= x: A + B = 0
= Constant: -A + 2B = 2
= 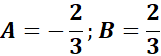
= 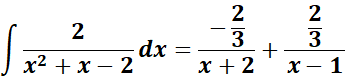
= 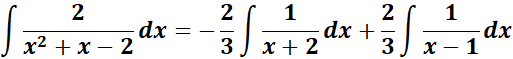
= 
= 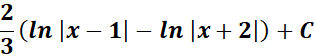
= Use the identity: 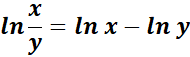
= 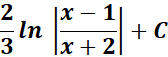
Answer: 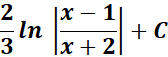
3. 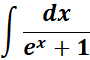
Steps:
a. The denominator must factored.
b. The partial fraction must be decomposition.
c. Use the denominator to multiply.
d. Expand, collect terms and solve the overall equation system.
e. Substitute the constants, integrate and find the non - repeated linear fraction.
Solution:
= 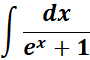
= u = ex; du = ex dx; dx = du/u
= 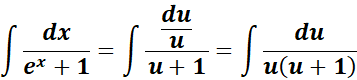
= 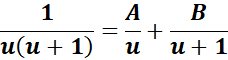
= ![]()
= ![]()
= Solve for A and B:
= u: A + B = 0
= Constant: A = 1
= A = 1; B = -1
= 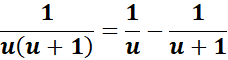
= 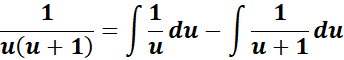
= 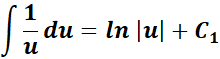
= 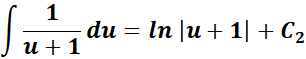
= ![]()
= Substitute the u:
= ![]()
Answer: ![]()
4. 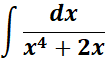
Steps:
a. The denominator must factored.
b. The partial fraction must be decomposition.
c. Use the denominator to multiply.
d. Expand, collect terms and solve the overall equation system.
e. Substitute the constants, integrate and find the non - repeated linear fraction.
Solution:
= 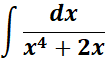
= Formula: 
= A = x; B = (x3 + 2)
= u = x3 + 2; du = 3x2 dx
= 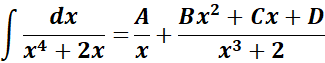
= 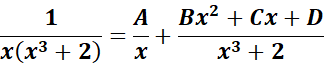
= ![]()
= ![]()
= Solve for A, B, C and D:
= x3: A + B = 0
= x2: C = 0
= x: D = 0
= Constant: 2A = 1
= 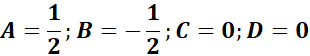
= 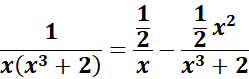
= 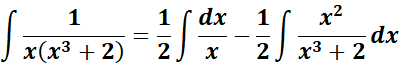
= 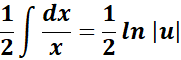
= 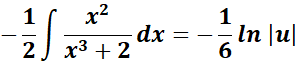
= 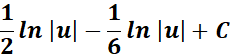
= Substitute the u:
= 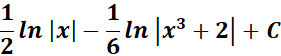
Answer: 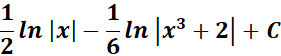
5. 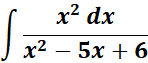
Steps:
a. The denominator must factored.
b. The partial fraction must be decomposition.
c. Use the denominator to multiply.
d. Expand, collect terms and solve the overall equation system.
e. Substitute the constants, integrate and find the non - repeated linear fraction.
Solution:
= 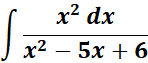
= Formula: 
= A = (x - 2); B = (x - 3)
= Rewrite the numerator: ![]()
= ![]()
= 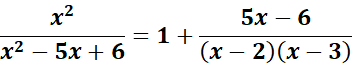
= 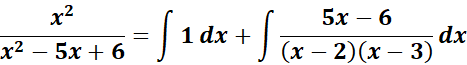
= 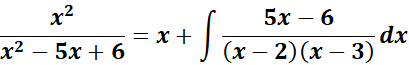
= 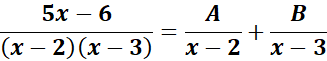
= ![]()
= ![]()
= Solve for A and B:
= x: A + B = 5
= Constant: -3A - 2B = 6
= A = -4; B = 9
= 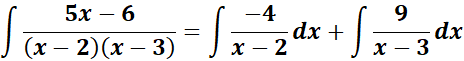
= 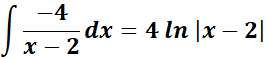
= 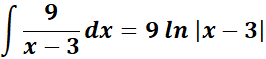
= Combine altogether:
= ![]()
Answer: ![]()
