| Non - Repeated Quadratic Factors |
Nov. 30, 2024, 6:27 p.m.
Definition
Non - Repeated Quadratic Factor
-> the polynomials of degree two that cannot be factored further into real linear factors.
Symbol:
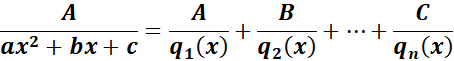
Where:
A, B, and C - constants to be determined.
qi(x) - represents the non - repeated quadratic factor.
ax2 + bx + c - denominator must be < 0.
Steps to use Non - Repeated Quadratic Factor |
1. Identify the denominator.
2. Set Up partial fractions for decomposition.
3. Multiply by the denominator.
4. Expand and collect terms to solve the coefficients.
5. Set up a system of equations and solve the constants.
6. Integrate and find the non - repeated quadratic factor.
Example |
1. Find the answer from this given:
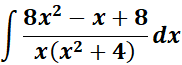
Steps:
1. The denominator must be identified.
2. Set Up partial fractions for decomposition.
3. Multiply by the denominator.
4. Expand and collect terms to solve the coefficients.
5. Set up a system of equations and solve the constants.
6. Integrate and find the non - repeated quadratic factor.
= 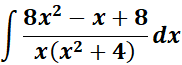
= A = x; B = (x2 + 4)
= Decomposition: 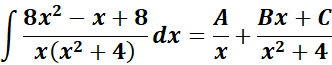
= ![]()
= ![]()
= Solve for A and B:
= x2: A + B = 8; x: C = -1
= Constants: 4A = 8
= A = 2; B = 6; C = -1
= 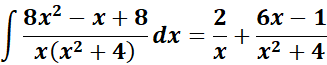
= Formula:  ;
; 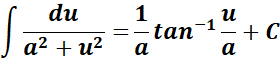
= 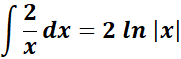
= 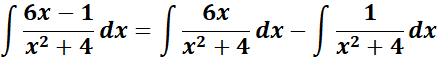
= u = x2 + 4; du = 2x dx; dx = du/2x
= 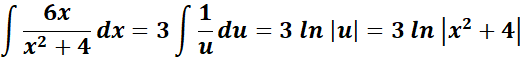
= 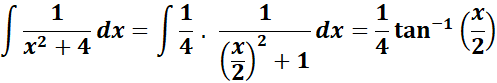
= Combine altogether:
= 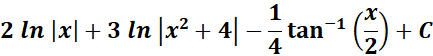
Exercises |
1. 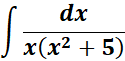
Steps:
a. The denominator must be identified.
b. Set Up partial fractions for decomposition.
c. Multiply by the denominator.
d. Expand and collect terms to solve the coefficients.
e. Set up a system of equations and solve the constants.
f. Integrate and find the non - repeated quadratic factor.
Solution:
= 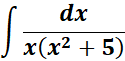
= Formula: 
= A = x; B = (x2 + 5)
= 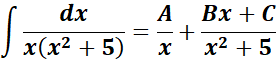
= ![]()
= ![]()
= Solve for A, B, and C:
= x2: A + B = 0; x: C = 0
= Constants: 5A = 1
= 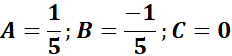
= 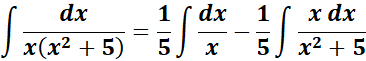
= 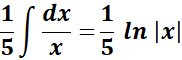
= u = x2 + 5; du = 2x dx
= 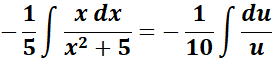 ;
; 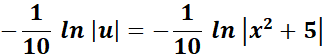
= Combine altogether:
= 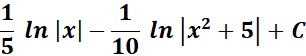
Answer: 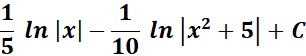
2. 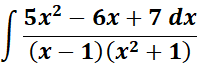
Steps:
a. The denominator must be identified.
b. Set Up partial fractions for decomposition.
c. Multiply by the denominator.
d. Expand and collect terms to solve the coefficients.
e. Set up a system of equations and solve the constants.
f. Integrate and find the non - repeated quadratic factor.
Solution:
= 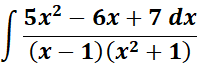
= Formula:  ;
; 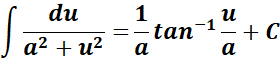
= A = (x - 1); B = (x2 + 1)
= 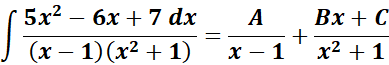
= ![]()
= ![]()
= Solve for A, B, and C:
= x2: A + B = 5; x = C - B = -6
= Constants: A - C = 7
= A = 3; B = 2; C = - 4
= 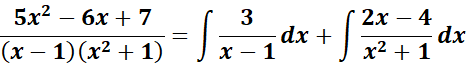
= 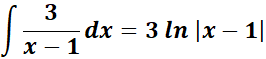
= 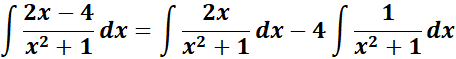
= 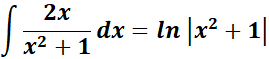
= 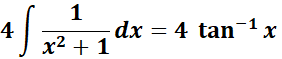
= Combine 1st: ![]()
= Combine altogether:
= ![]()
Answer: ![]()
3. 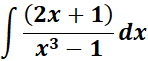
Steps:
a. The denominator must be identified.
b. Set Up partial fractions for decomposition.
c. Multiply by the denominator.
d. Expand and collect terms to solve the coefficients.
e. Set up a system of equations and solve the constants.
f. Integrate and find the non - repeated quadratic factor.
Solution:
= 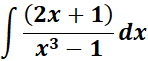
= Formula: 
= A = (x - 1); B = (x2 + x + 1)
= Rewrite: 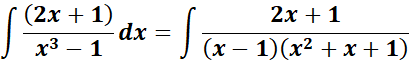
= ![]()
= 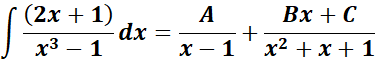
= ![]()
= ![]()
= Solve for A, B, and C:
= x2: A + B = 0; x: A + C - B = 2
= Constants: A - C = 1
= A = 1; B = - 1 ; C = 0
= 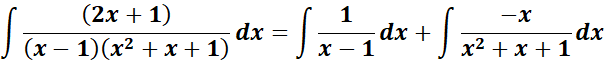
= 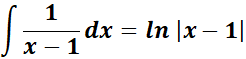
= 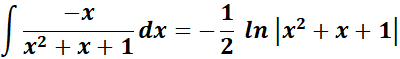
= Combine altogether:
= 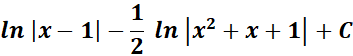
Answer: 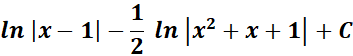
4. 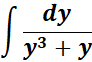
Steps:
a. The denominator must be identified.
b. Set Up partial fractions for decomposition.
c. Multiply by the denominator.
d. Expand and collect terms to solve the coefficients.
e. Set up a system of equations and solve the constants.
f. Integrate and find the non - repeated quadratic factor.
Solution:
= 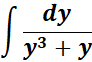
= Formula: 
= A = y; B = (y2+ 1)
= Rewrite: 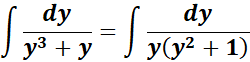
= ![]()
= 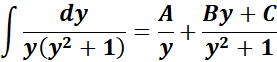
= ![]()
= ![]()
= Solve for A, B, and C:
= y2: A + B = 0; y = C = 0
= Constants: A = 1
= A = 1; B = -1; C = 0
= 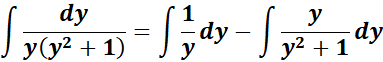
= 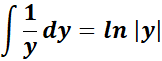
= 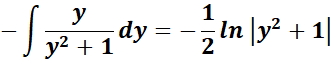
= Combine altogether:
= 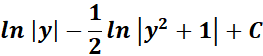
Answer: 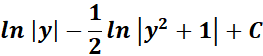
5. 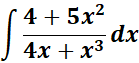
Steps:
a. The denominator must be identified.
b. Set Up partial fractions for decomposition.
c. Multiply by the denominator.
d. Expand and collect terms to solve the coefficients.
e. Set up a system of equations and solve the constants.
f. Integrate and find the non - repeated quadratic factor.
Solution:
= 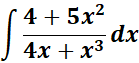
= Formula: 
= A = x; B = (4 + x2)
= Rewrite: 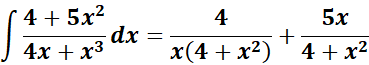
= ![]()
= Integrate each term: 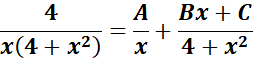
= ![]()
= ![]()
= Solve for A, B, and C:
= x2: A + B = 0; x = C = 0
= Constants: 4A = 4
= A = 1; B = -1; C = 0
= 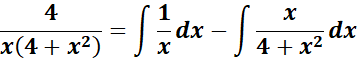
= 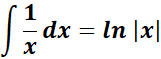 ;
; 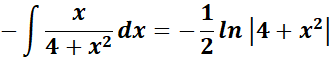
= u = 4 + x2; du = 2x dx
= 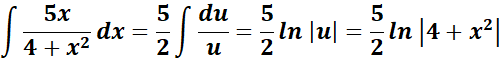
= Combine altogether:
= 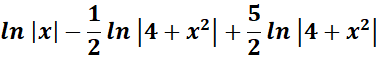
= ![]()
Answer: ![]()
