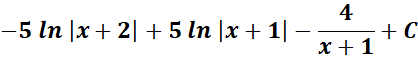| Repeated Linear Factors |
Nov. 30, 2024, 6:23 p.m.
Definition
Repeated Linear Fraction
-> the denominator is repeated.
Symbol:
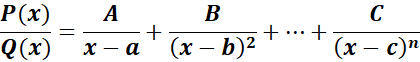
Where:
A, B, and C - constants to be determined.
Steps to use Repeated Linear Fraction |
1. Factor the denominator.
2. Set Up partial fractions for decomposition.
3. Combine fractions by multiply using the denominator.
4. Expand and collect terms to solve the coefficients.
5. Write the decomposed integral.
6. Integrate and find the repeated linear fractions.
Example |
1. Find the answer from this given:
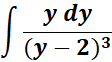
Steps:
1. The denominator must factored.
2. The partial fraction must be decomposition.
3. Use the denominator to multiply.
4. Expand, collect terms and solve the overall equation system.
5. Substitute the constants, integrate and find the repeated linear fraction.
= 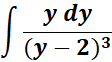
= A = (y - 2); B = (y - 2)2; C = (y - 2)3
= 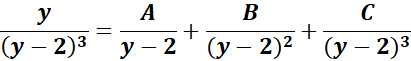
= ![]()
= ![]()
= Solve for A, B and C:
= y2: A = 0
= y: B - 4A = 1
= Constants: 4A − 2B + C=0
= A = 0; B = 1; C = 2
= 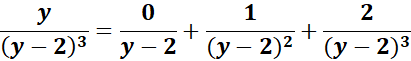
= 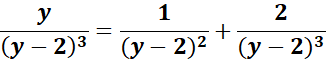
= 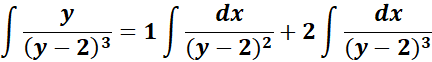
= u = y - 2; du = dy
= Formula: 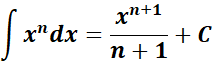
= 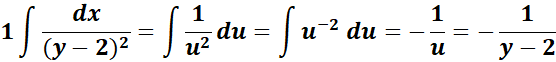
= 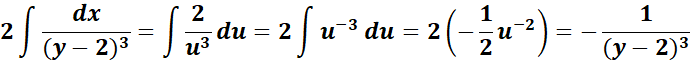
= 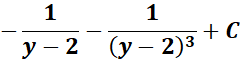
Exercises |
1. 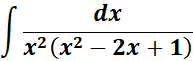
Steps:
a. The denominator must factored.
b. The partial fraction must be decomposition.
c. Use the denominator to multiply.
d. Expand, collect terms and solve the overall equation system.
e. Substitute the constants, integrate and find the repeated linear fraction.
Solution:
= 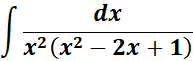
= Formula: 
= A = x; B = x2; C = (x - 1); D = (x - 1)2
= ![]()
= ![]()
= 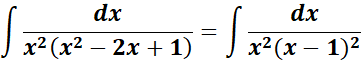
= 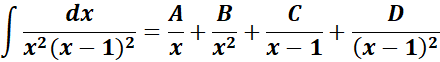
= Solve for A, B, C, and D:
= x3: A + C = 0
= x2: -2A + B - C + D = 0
= x: A - 2B = 0
= Constants: B = 1
= A = 2; B = 1; C = -2; D = 1
= 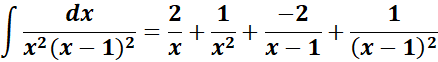
= 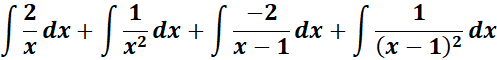
= 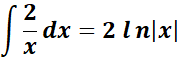 ;
; 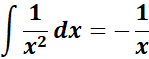
= 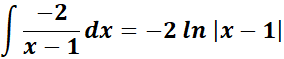 ;
; 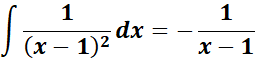
= Combine altogether:
= 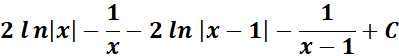
Answer: 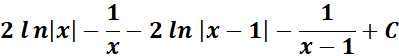
2. 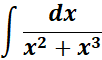
Steps:
a. The denominator must factored.
b. The partial fraction must be decomposition.
c. Use the denominator to multiply.
d. Expand, collect terms and solve the overall equation system.
e. Substitute the constants, integrate and find the repeated linear fraction.
Solution:
= 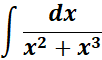
= Formula: 
= A = x; B = x2; C = (1 + x)
= 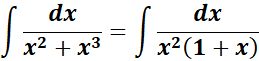
= 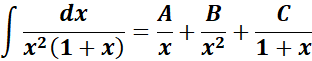
= ![]()
= ![]()
= Solve for A, B, and C:
= x2: A + C = 0
= x: A + B = 0
= Constants: B = 1
= A = -1; B = 1; C = 1
= 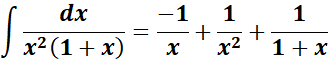
= 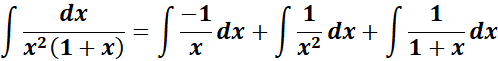
= 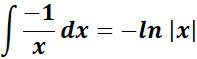 ;
; 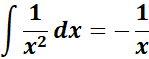
= 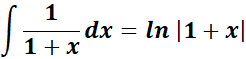
= Combine altogether:
= 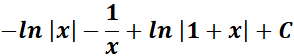
Answer: 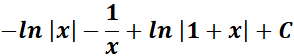
3. 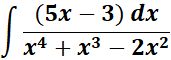
Steps:
a. The denominator must factored.
b. The partial fraction must be decomposition.
c. Use the denominator to multiply.
d. Expand, collect terms and solve the overall equation system.
e. Substitute the constants, integrate and find the repeated linear fraction.
Solution:
= 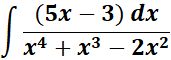
= Formula: 
= A = x; B = x2; C = (x - 1); D = (x + 2)
= 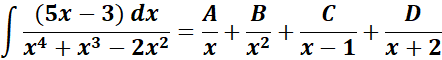
= ![]()
= ![]()
= Solve for A, B, C, and D:
= x3: A + C + D = 0; x2: A + B + 2C - D = 0
= x: -2A + B = 5; Constants: -2B = -3
= 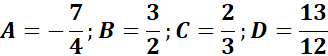
= 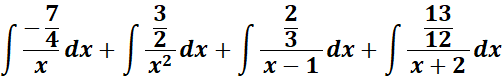
= 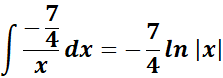 ;
; 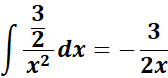
= 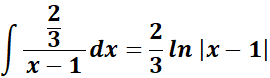 ;
; 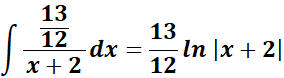
= Combine altogether:
= 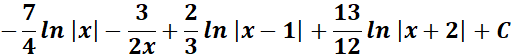
Answer: 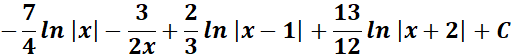
4. 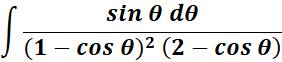
Steps:
a. The denominator must factored.
b. The partial fraction must be decomposition.
c. Use the denominator to multiply.
d. Expand, collect terms and solve the overall equation system.
e. Substitute the constants, integrate and find the repeated linear fraction.
Solution:
= 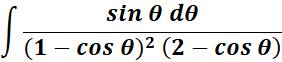
=Formula: 
= 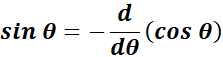
= Rewrite: 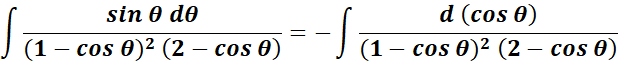
= ![]()
= 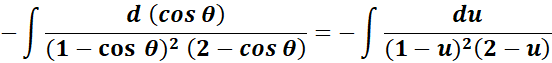
= A = (1 - u); B = (1 - u)2; C = (2 - u)
= 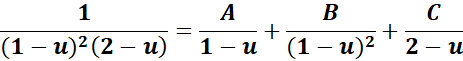
= ![]()
= ![]()
= Solve for A, B, and C:
= u2: A + C = 0; u = -3A - B - 2C = 0
= Constants: 2A +2B + C = 1
= A = -1; B = 1; C = 1
= 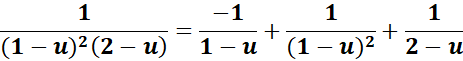
= 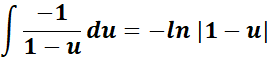
= 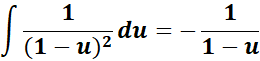
= 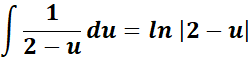
= Combine altogether and substitute the u:
= 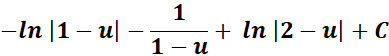
= 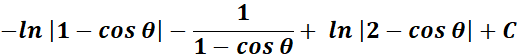
Answer: 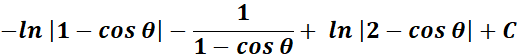
5. 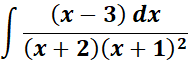
Steps:
a. The denominator must factored.
b. The partial fraction must be decomposition.
c. Use the denominator to multiply.
d. Expand, collect terms and solve the overall equation system.
e. Substitute the constants, integrate and find the repeated linear fraction.
Solution:
= 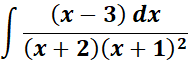
= Formula: 
= A = (x + 2); B = (x + 1); C = (x +1)2
= 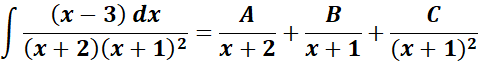
= ![]()
= ![]()
= Solve for A, B, and C:
= x2: A + B = 0; x: 2A + 2B + C = 1
= Constants: A + 2B + 2C = -3
= A = -5; B = 5; C = 4
= 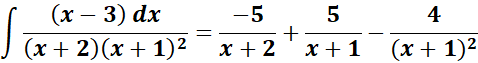
= 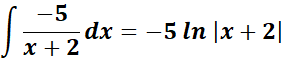
= 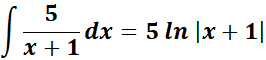
= 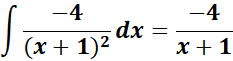
= Combine altogether:
= 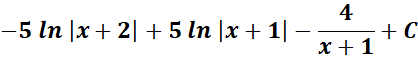
Answer: