Definition
Derivative of a Function
-> the limit of the ratio of the increment function to the increment of independent variable when it varies and approaches zero.
-> also known as instantaneous rate of change.
Symbol:
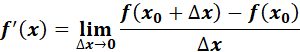
Where:
The derivative of a function f at a number x.
General Rules for Differentiation |
1. In the original equation, replace x with 
, and y with 
, and simplify.
2. Subtract the original equation from the new equation, thus obtaining 
in terms of x and 
and simplify.
3. Divide both members of the equation by 
and simplify.
4. Find the limit of both sides of the equation as 
.
Example |
1. Find the answer from this given:
Steps:
a. Substitute the x with 
and 
.
b. Rearrange with the same value, where the must be at the left, while the rest at the right side.
c. Substitute the y equivalent.
d. Factor out the 
.
e. Substitute the 
with 0.
f. Find the limit.
= 
= 
= 
= 
= 
= 
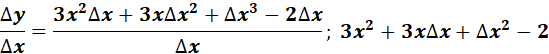
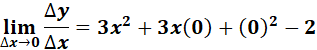
= 3x2 - 2
Exercises |
1. x = y4 - 2y3
Steps:
a. Use the derivative of a function.
b. Substitute the x and y with and .
c. Rearrange with the same value, where the must be at the left, while the rest at the right side.
d. Substitute the x equivalent.
e. Factor out the .
f. Substitute the with 0.
g. Find the limit.
Solution:
= x = y4 - 2y3
= 
= 
= 
= 
= 
= 
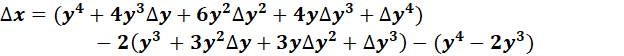
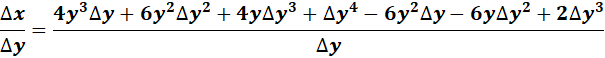
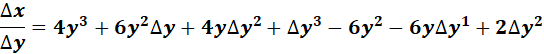
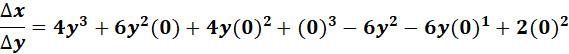
= 4y3 - 6y2
Answer: 4y3 - 6y2
2. 
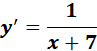
Steps:
a. Use the derivative of a function.
b. Substitute the x and y with and .
c. Rearrange with the same value, where the must be at the left, while the rest at the right side.
d. Substitute the y equivalent.
e. Factor out the .
f. Substitute the with 0.
g. Find the limit.
Solution:
=
= 
= 
= 
= 
= 
= 
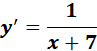
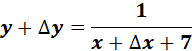
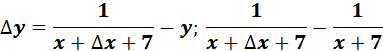
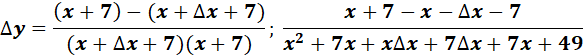
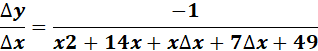
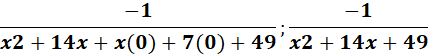
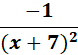
Answer: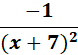
3. 
Steps:
a. Use the derivative of a function.
b. Substitute the m and n with 
and m with 
.
c. Rearrange with the same value, where the 
must be at the left, while the rest at the right side.
d. Substitute the m equivalent.
e. Factor out the .
f. Substitute the with 0.
g. Find the limit.
Solution:
=
= 
= 
= 
= 
= 
= 
= 
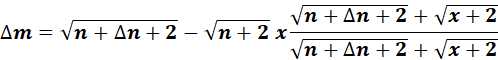
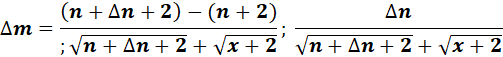
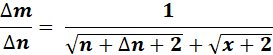
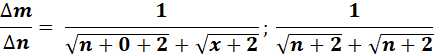
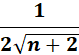
Answer: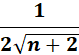
4. 
Steps:
a. Use the derivative of a function.
b. Substitute the a and b with 
and 
.
c. Rearrange with the same value, where the 
must be at the left, while the rest at the right side.
d. Substitute the b equivalent.
e. Factor out the .
f. Substitute the with 0.
g. Find the limit.
Solution:
=
= 
= 
= 
= 
= 
= 
= 
= 
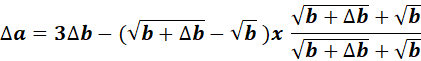
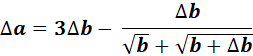
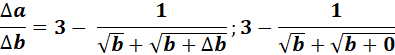
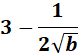
Answer: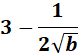
5. g = cos h
Steps:
a. Use the derivative of a function.
b. Substitute the g and h with 
and 
.
c. Rearrange with the same value, where the 
must be at the left, while the rest at the right side.
d. Substitute the g equivalent.
e. Factor out the .
f. Substitute the with 0.
g. Find the limit.
Solution:
= g = cos h
= 
= 
= 
= 
= 
= 
= 
= 
= 
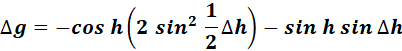
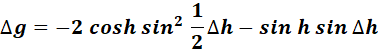
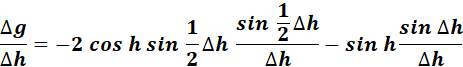
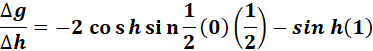
= - sin h
Answer: - sin h