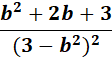Definition
Derivative of a Variable
-> it is equal to the increment of that variable.
Formulas of Derivative - I |
1. Constant Derivative
-> the derivative of constant must be zero.
Formula: y = c
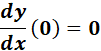
2. Power Derivative
-> the derivative of nth power of a function is equal to n times the product of the (n-1)th power function and function derivative.
Formula: y = xn
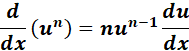
3. Function with Respect to Itself Derivative.
-> the derivative of a variable with respect to itself is one.
Formula: y = x
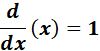
4. Sum Derivative.
-> the derivative of a sum of two/more functions is equal tot he sum of their derivatives, then the rest.
Formula: y = u + v - w
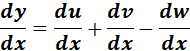
5. Product and Constant Product Derivative
-> the derivative of a product of functions is the first function times the derivative of the second, plus the second function times the derivative of the first.
-> the derivative of a constant times a function is the constant times the derivative of the function.
Formula: y = u . v
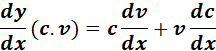
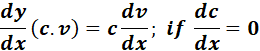
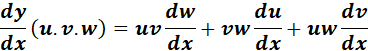
6. Quotient and Constant Quotient Derivative.
-> the derivative of a quotient of two functions, subtract the numerator multiplied by the derivative of the denominator from the denominator multiplied by the derivative of the numerator, all divided by the square of the denominator.
-> the derivative of a constant divided by a function is the negative constant times the derivative of the function, divided by the square of the function.
Formula: y = u/v
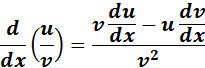
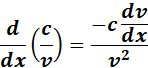
7. Square Root Derivative.
-> The derivative of the square root of a function is the derivative of the function divided by twice the square root of the function.
Formula: y = un
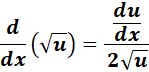
Example |
1. Find the answer from this given:
y = x4
Steps:
a. Write the d/dx first.
b. Use the specific derivative formula.
c. Find the dy/dx.
= y = x4
= u = x; n = 4
= 
= 
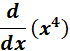
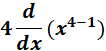
= 4x3
Exercises |
1. y = ax3 - bx2
Steps:
a. Write the d/dx first.
b. Use the specific derivative formula.
c. Find the dy/dx.
Solution:
= y = ax3 - bx2
= Constant: a & b; n: 3 & 2
= Formula: ;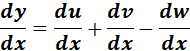 
= 
= 
= 
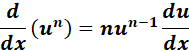
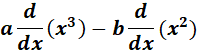
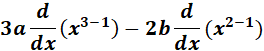
= 3ax2 - 2bx
Answer: 3ax2 - 2bx
2. 
Steps:
a. Write the d/dn first.
b. Use the specific derivative formula.
c. Find the dm/dn.
Solution:
=
= Constants: 5, -4, 7 & 1; n: 3 & 5
= Formula: ;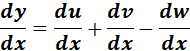
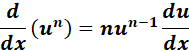
= Constants: 3, -7 & 4; n: 13/5 & -1/3
= 
= 
= 
= 
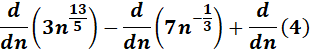
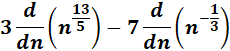
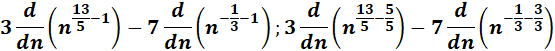
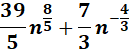
Answer: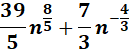
3. y = 5 - 4x + 7x3 - x5
Steps:
a. Write the d/dx first.
b. Use the specific derivative formula.
c. Find the dy/dx.
Solution:
= y = 5 - 4x + 7x3 - x5
= Constants: 5, -4, 7 & -1; n: 3 & 5
= Formula: ;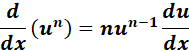
= 
= 
= 
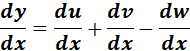
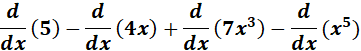
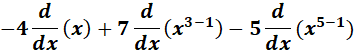
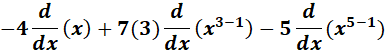
= -4 + 21x2 - 5x4
Answer: -4 + 21x2 - 5x4
4. y = (1 + x3)(3 - 2x)
Steps:
a. Factor them together and find the complete equation.
b. Write the d/dx first.
c. Use the specific derivative formula.
d. Find the dy/dx.
Solution:
= y = (1 + x3)(3 - 2x)
= Rewrite: y = 3 - 2x + 3x3 - 2x4
= Constants: 3, -2, 3 and & -2; n = 1, 3 & 4
= Formula: ;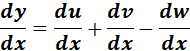
= 
= 
= 
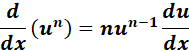
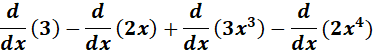
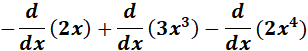
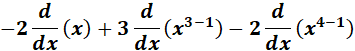
= -2 + 9x2 - 8x3
Answer: -2 + 9x2 - 8x3
5. 
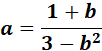
Steps:
a. Write the d/db first.
b. Use the specific derivative formula.
c. Find the da/db.
Solution:
=
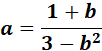
= u: 1+b; v: 3 - b2
= Formula: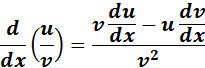
= 
= 
= 
= 
= 
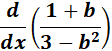
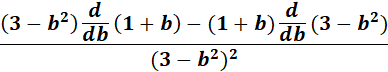
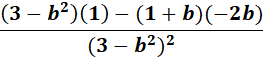
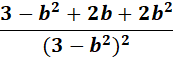
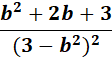
Answer: