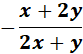Formulas of Derivative - II
1. Chain Rule Derivative
-> The derivative of finding the derivative of the outer function with respect to the input, we multiply it by the derivative of the inner function with respect to the independent variable.
-> The derivative is equal to the quotient of the derivatives from dependent variable over the independent variable.
-> The derivative of inverse is equal to the reciprocal of the derivative of the direct function.
Formula: y = f(u): where u = g(x).
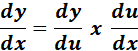
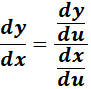
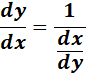
2. Implicit Derivative
-> The derivative where the equation in x and y is given, but not solve for y.
Formula: Nothing, but the y must be place on the other side.
3. Parametric Equation Derivative
-> The derivative where the equation in x and y is given, but not solve for y.
Formula: x = f(x, y = g(t)).
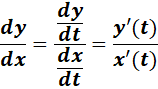
Example |
1. Find the answer from this given:
y = u2 + 6u - 2; u = 4x2 + 8x + 1
Steps:
a. Write the d/dx first.
b. Use the specific derivative formula.
c. Find the dy/dx.
= y = u2 + 6u - 2 ; u = 4x2 + 8x + 1
= 
= 
= 
= 
= 
= 
= 
= 
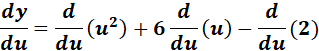
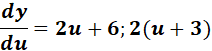
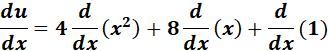
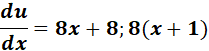
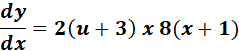
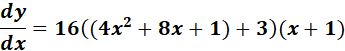
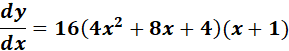
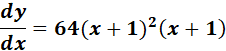
= 64 (x + 1)3
Exercises |
1. x3 + y3 = a3
Steps:
a. Write the d/dx first.
b. Use the specific derivative formula.
c. Find the d/dx.
Solution:
= x3 + y3 = a3
= Formula: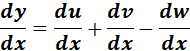 
; 
= 
= 
= 
= 
= 
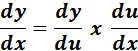
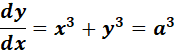
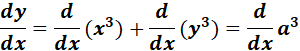
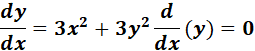
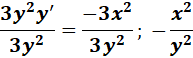
Answer: 
2. 
Steps:
a. Write the d/dx first.
b. Use the specific derivative formula.
c. Find the d/dx.
Solution:
=
= Formula: ;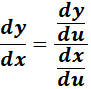 
;
= 
= 
= 
= 
= 
= 
= 
= 
= 
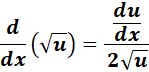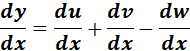
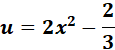
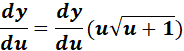
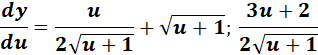
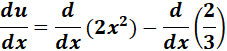
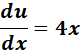
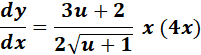
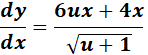
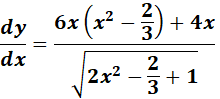
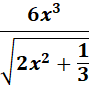
Answer: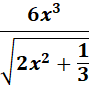
3. x = t3 - 2t + 1; y = t2 + 3t - 2
Steps:
a. Write the dx/dt first.
b. Use the specific derivative formula.
c. Find the dx/dt.
Solution:
= x = t3 - 2t + 1; y = t2 + 3t - 2
= Formula: ; ;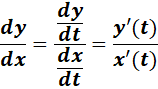 
= 
= 
= 
= 
= 
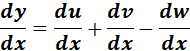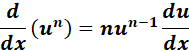
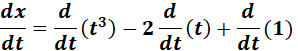
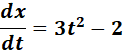
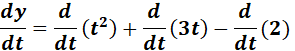
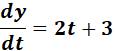
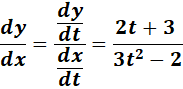
Answer: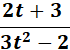 
4. 
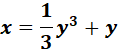
Steps:
a. Write the d/dx first.
b. Use the specific derivative formula.
c. Find the dy/dx.
Solution:
=
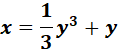
= Formula: ; ;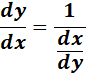
= 
= 
= 
= 
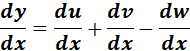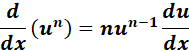
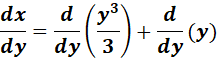
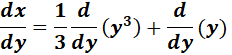
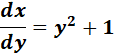
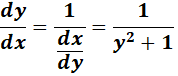
Answer: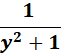 
5. x2 + y2 = 2xy
Steps:
a. Write the d/dx first.
b. Use the specific derivative formula.
c. Find the dy/dx.
Solution:
= x2 + y2 = 2xy
= Formula: ; ;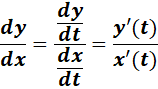
= 
= 
= 
= 
= 
= 
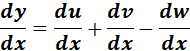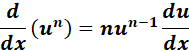
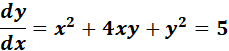
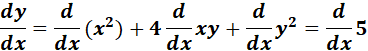
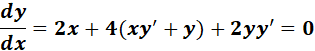
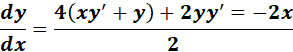
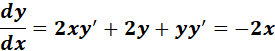
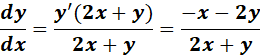
Answer: 