Definition
Higher Derivative
-> The derivative after the first, the second order of derivative, third order of derivative and so on.
Symbol:
Where:
The derivative of a higher.
Example |
1. Find the fourth derivative from this given:
y = 3x4 - 2x3 + 5
Steps:
a. Write the d/dx first.
b. Use the specific derivative formula.
c. Find the dy/dx.
d. Continue to derivative based on the given.
= y = 3x4 - 2x3 + 5
= 
= 
; 
= 
; 
= 
; 
= 
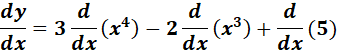
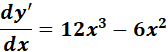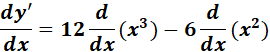
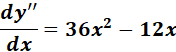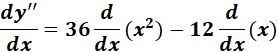
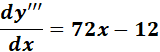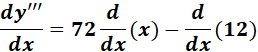
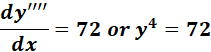
= y4 = 72
Exercises |
1. 4x2 - 9y2 = 36; 2nd Derivative of Implicit
Steps:
a. Write the d/dx first.
b. Use the specific derivative formula.
c. Find the dy/dx.
d. Continue to derivative based on the given.
Solution:
= 4x2 - 9y2 = 36
= Formula: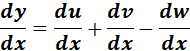 
; 
= 
= 
= 
= 
= 
= 
= 
= 
= 
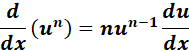
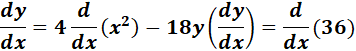
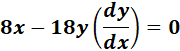
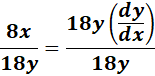
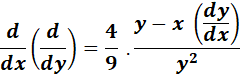
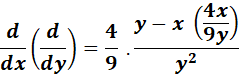
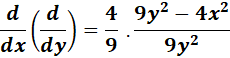
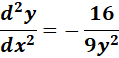
Answer: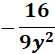 
2. u3 = a2t; 2nd Derivative
Steps:
a. Write the du/dt first.
b. Use the specific derivative formula.
c. Rearrange the given.
d. Find the du/dt.
e. Continue to derivative based on the given.
Solution:
= u3 = a2t
= Formula: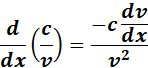 
= 
= 
= 
= 
= 
= 
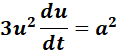
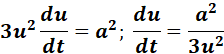
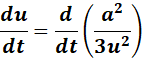
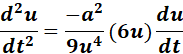
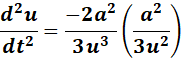
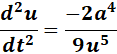
Answer: 
3. m = n5 - 3n7 - 2n + 5; 3rd Derivative
Steps:
a. Write the dm/dn first.
b. Use the specific derivative formula.
c. Find the dm/dn.
d. Continue to derivative based on the given.
Solution:
= m = n5 - 3n7 - 2n + 5
= Formula: ;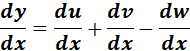
= 
= 
= 
= 
= 
= 
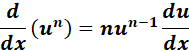
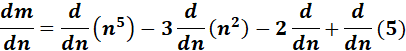
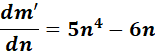
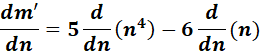
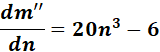
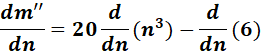
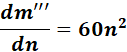
Answer: 
4. a = cos b; 4th Derivative of Trigonometric
Steps:
a. Write the d/dx first.
b. Use the specific derivative formula.
c. Find the dy/dx.
d. Continue to derivative based on the given.
Solution:
= a = cos b
= Formula: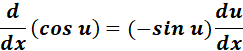 
; 
= 
= 
= 
= 
= 
= 
= 
= 
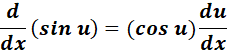
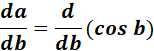
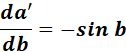
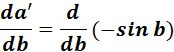
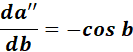
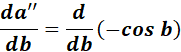
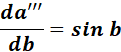
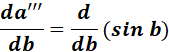
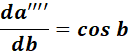
Answer: cos b
5. q = sec (5t); 2nd Derivative of Trigonometric
Steps:
a. Write the d/dx first.
b. Use the specific derivative formula.
c. Find the dy/dx.
d. Continue to derivative based on the given.
e. Use trigonometric identities.
Solution:
= q = sec (5t)
= Formula: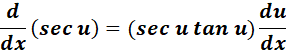 
; 
= 
= 
= 
= 
= 
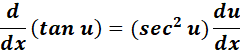
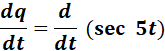
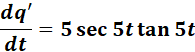
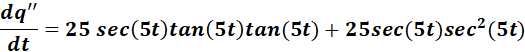
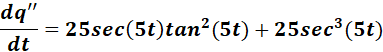
Answer: 25 sec (5t) tan2 (5t) + 25 sec3 (5t)