Definition
Integral of Exponential Functions
-> this refers to integrate the exponential.
Formulas of Integral of Exponential Functions |
1. eax Integral
-> this states the a is constant, and C is the constant of integration.
Formula:
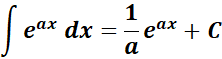
2. ax Integral (a must be positive and constant is not equal to 1)
-> this states the a > 0, and a not equal to 1, the ln (a) is the natural logarithm of ?, and C is constant of integration.
Formula:
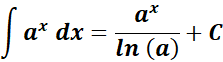
Example |
1. Find the answer from this given:
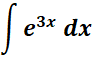
Steps:
a. Write the given 1st.
b. Use the specific exponential integral formula.
c. Find the exponential integral.
=
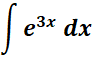
= v = 3x; dv = d(3x) = 3 dx; a = 3
= Formula: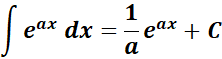
= 
= 
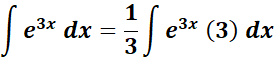
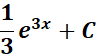
Exercises |
1. 
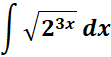
Steps:
a. Write the given 1st.
b. Use the specific exponential integral formula.
c. Find the exponential integral.
Solution:
=
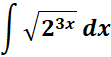
= Formula: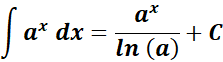
= Rewrite: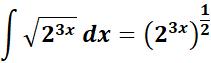 
= Use the property: (ab)c = abc; 
= New Given: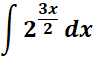 
= a = ; 
= 
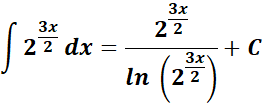
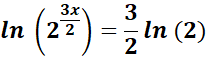
= Simplify: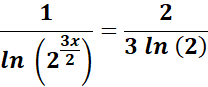 
= Combine the computations:
= 
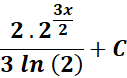
Answer: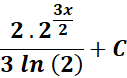
2. 
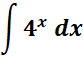
Steps:
a. Write the given 1st.
b. Use the specific exponential integral formula.
c. Find the exponential integral.
Solution:
=
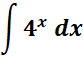
= Use this: 
= New Given: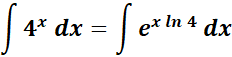 
= Formula: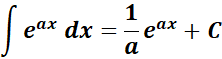
= 
= 
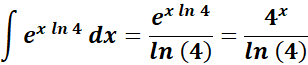
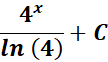
Answer: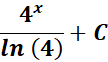
3. 
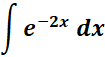
Steps:
a. Write the given 1st.
b. Use the specific exponential integral formula.
c. Find the exponential integral.
Solution:
=
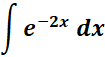
= Formula: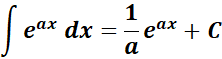
= a = -2
= 
= 
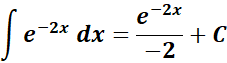
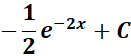
Answer: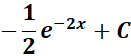
4. 
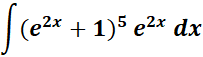
Steps:
a. Write the given 1st.
b. Use the specific exponential integral formula.
c. Find the exponential integral.
Solution:
=
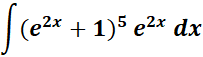
= u = e2x + 1; du = 2 e2x dx
= 
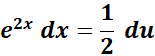
= Rewrite: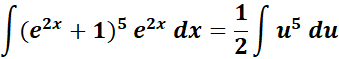 
= Formula: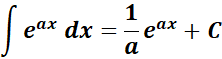
= 
= 
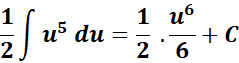
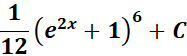
Answer: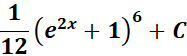
5. 
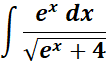
Steps:
a. Write the given 1st.
b. Use the specific exponential integral formula.
c. Find the exponential integral.
Solution:
=
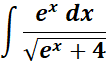
= Formula: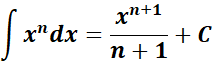 
= u = ex + 4; du = ex dx
= Use the u to substitute: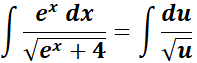 
= 
= 
= 
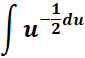
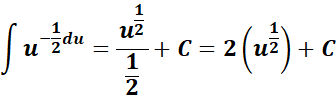
Answer: