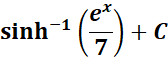Definition
Integral of Inverse Hyperbolic Functions
-> this refers to integrate the inverse hyperbolic.
Formulas of Integral of Inverse Hyperbolic Functions |
1. Inverse Hyperbolic Sine Integral
-> this states the integral of inverse hyperbolic sine function.
Formula:
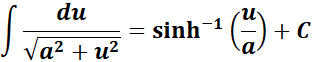
2. Inverse Hyperbolic Cosine Integral
-> this states the integral of inverse hyperbolic cosine function.
Formula:
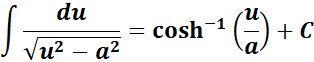
3. Inverse Hyperbolic Tangent Integral
-> this states the integral of inverse hyperbolic tangent function if u2 < a2.
Formula:
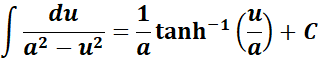
4. Inverse Hyperbolic Cotangent Integral
-> this states the integral of inverse hyperbolic cotangent function if u2 > a2.
Formula:
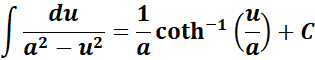
5. Inverse Hyperbolic Secant Integral
-> this states the integral of inverse hyperbolic secant function.
Formula:
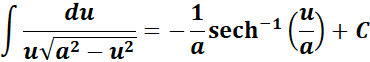
6. Inverse Hyperbolic Cosecant Integral
-> this states the integral of inverse hyperbolic cosecant function.
Formula:
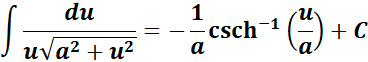
Example |
1. Find the answer from this given:
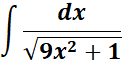
Steps:
a. Write the given 1st.
b. Use the specific inverse hyperbolic trigonometric integral formula.
c. Find the inverse hyperbolic trigonometric integral.
=
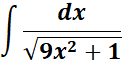
= u = 3x; du = 3 dx
= Formula: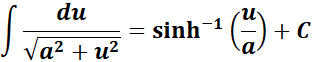
= 
= 
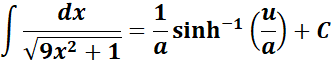
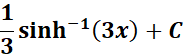
Exercises |
1. 
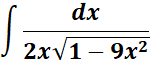
Steps:
a. Write the given 1st.
b. Use the specific inverse hyperbolic trigonometric integral formula.
c. Find the inverse hyperbolic trigonometric integral.
Solution:
=
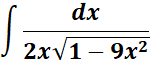
= Formula: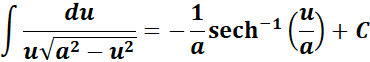
= u = 3x; du = 3 dx; a = 1
= 
= 
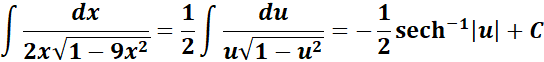
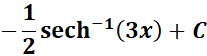
Answer: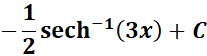
2. 
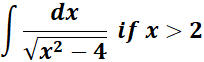
Steps:
a. Write the given 1st.
b. Use the specific inverse hyperbolic trigonometric integral formula.
c. Find the inverse hyperbolic trigonometric integral.
Solution:
=
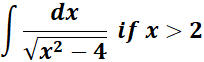
= Formula: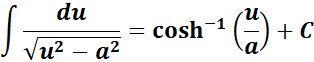
= a2 = 4; a = 4
= 
= 
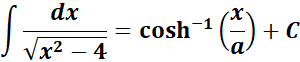
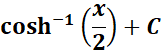
Answer: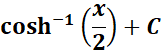
3. 
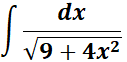
Steps:
a. Write the given 1st.
b. Use the specific inverse hyperbolic trigonometric integral formula.
c. Find the inverse hyperbolic trigonometric integral.
Solution:
=
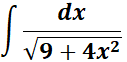
= Formula: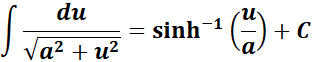
= a2 = 9; a = 3; u2 = 4x2; u = 2x
= 
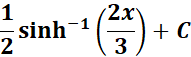
Answer: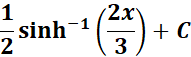
4. 
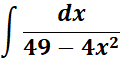
Steps:
a. Write the given 1st.
b. Use the specific inverse hyperbolic trigonometric integral formula.
c. Find the inverse hyperbolic trigonometric integral.
Solution:
=
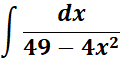
= Formula: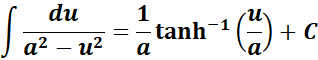 
= a2 = 49; a = 7; u2 = 4x2; u = 2x
= 
= 
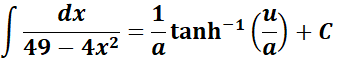
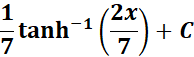
Answer: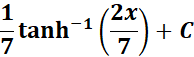
5. 
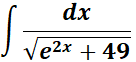
Steps:
a. Write the given 1st.
b. Use the specific inverse hyperbolic trigonometric integral formula.
c. Find the inverse hyperbolic trigonometric integral.
Solution:
=
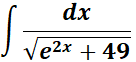
= Formula: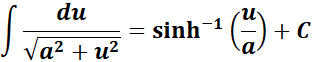
= u = ex; du = ex dx; dx = du/u; a2 = 49; a = 7
= 
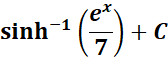
Answer: