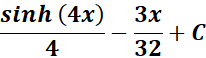Definition
Integral of Hyperbolic Functions
-> this refers to integrate the hyperbolic functions.
Formulas of Integral of Hyperbolic Functions |
1. Hyperbolic Sine Integral
-> this states the integral of hyperbolic sine function.
Formula:
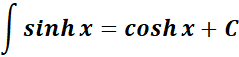
2. Hyperbolic Cosine Integral
-> this states the integral of hyperbolic cosine function.
Formula:
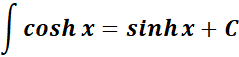
3. Hyperbolic Secant2 Integral
-> this states the integral of hyperbolic secant2 function.
Formula:
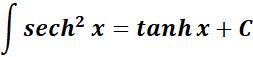
4. Hyperbolic Cosecant2 Integral
-> this states the integral of hyperbolic cosecant2 function.
Formula:
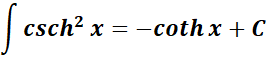
5. Hyperbolic Secant & Tangent Integral
-> this states the integral of hyperbolic secant & tangent function.
Formula:
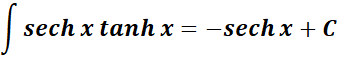
6. Hyperbolic Cosecant & Cotangent Integral
-> this states the integral of hyperbolic cosecant & cotangent function.
Formula:
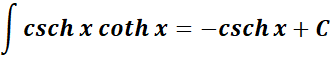
7. Hyperbolic Tangent Integral
-> this states the integral of hyperbolic tangent function.
Formula:
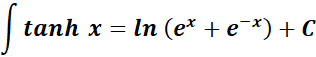
8. Hyperbolic Cotangent Integral
-> this states the integral of hyperbolic cotangent function.
Formula:
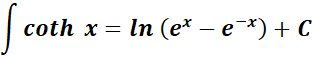
9. Hyperbolic Secant Integral
-> this states the integral of hyperbolic secant function.
Formula:
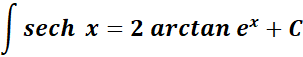
10. Hyperbolic Cosecant Integral
-> this states the integral of hyperbolic cosecant function.
Formula:
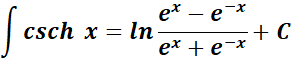
Example |
1. Find the answer from this given:
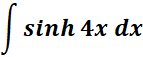
Steps:
a. Write the given 1st.
b. Use the specific hyperbolic trigonometric integral formula.
c. Find the hyperbolic trigonometric integral.
=
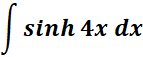
= a = 4
= Formula: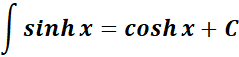
= 
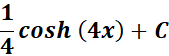
Exercises |
1. 
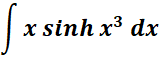
Steps:
a. Write the given 1st.
b. Use the specific hyperbolic trigonometric integral formula.
c. Find the hyperbolic trigonometric integral.
Solution:
=
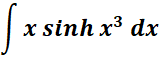
= Formula: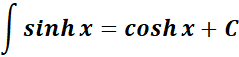
= u = x3; du = 3x2 dx; x2 dx = du/3x2
= Solve x2: x2 = u2/3
= New Given: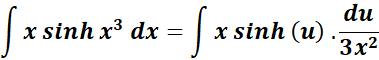 
= Simplify: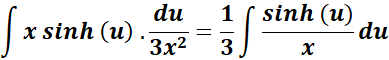 
= Substitute the x: x = u1/3; 1/x = u-1/3 du
= 
= 
= 
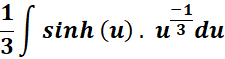
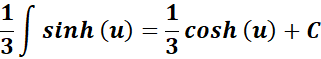
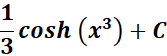
Answer: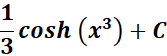
2. 
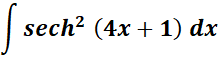
Steps:
a. Write the given 1st.
b. Use the specific hyperbolic trigonometric integral formula.
c. Find the hyperbolic trigonometric integral.
Solution:
=
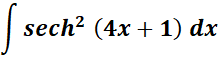
= Formula: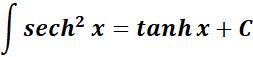
= u = 4x + 1; du = 4 dx; dx = du/4
= New Given: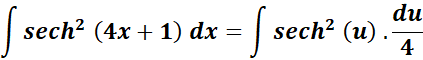 
= 
= 
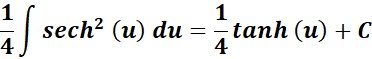
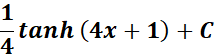
Answer: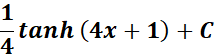
3. 
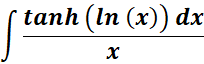
Steps:
a. Write the given 1st.
b. Use the specific hyperbolic trigonometric integral formula.
c. Find the hyperbolic trigonometric integral.
Solution:
=
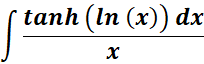
= Formula: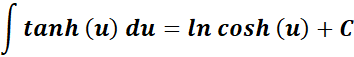 
= u = ln (x); du = dx/x; dx = x du
= New Given: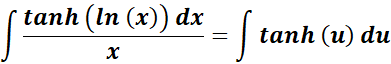 
= 
Answer:
4. 
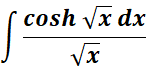
Steps:
a. Write the given 1st.
b. Use the specific hyperbolic trigonometric integral formula.
c. Find the hyperbolic trigonometric integral.
Solution:
=
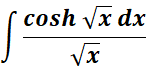
= Formula: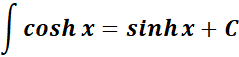
= u = 
; du =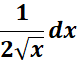 
; 
= New Given: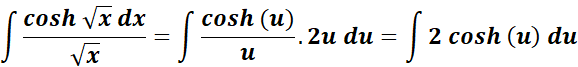 
= 
Answer:
5. 
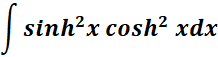
Steps:
a. Write the given 1st.
b. Use the specific hyperbolic trigonometric integral formula.
c. Use Hyperbolic Identities.
c. Find the hyperbolic trigonometric integral.
Solution:
=
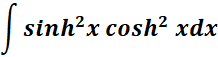
= Formula: ;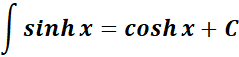
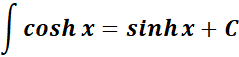
= Use Hyperbolic Identities: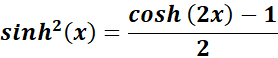 
;
= 
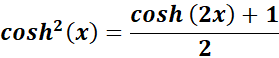
= Substitute: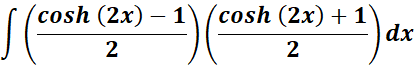 
= Simplify: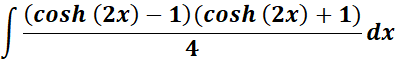 
= 
= New Given: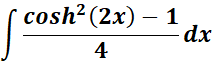 
= 
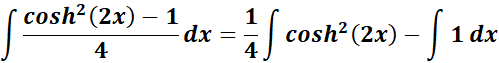
= Use this to integrate: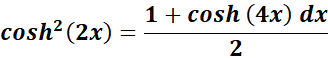 
= 
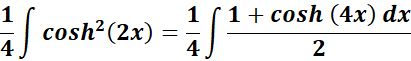
= Simplify: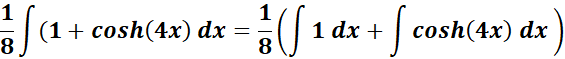 
= 
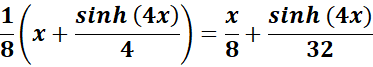
= Combine: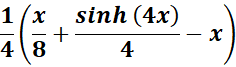 
= 
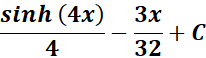
Answer: