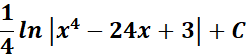Definition
Integral of Logarithm Functions
-> this refers to integrate the logarithm.
Formulas of Integral of Logarithm Functions |
1. 
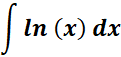Integral
-> the integral of natural log function is the log to the base e.
Formula:
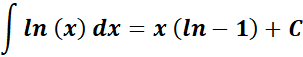
2. 
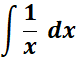Integral
-> the integral of 1/x is equal to natural log functions.
Formula:
3. 
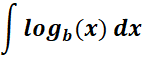Integral
-> it must convert first to the natural log and apply integration.
Formula:
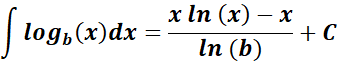
Example |
1. Find the answer from this given:
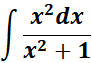
Steps:
a. Write the given 1st.
b. Use the specific logarithm integral formula.
c. Find the logarithm integral.
=
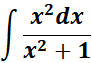
= v = x3 + 1; dv = d(x3 +1) = 3x2 dx
= Formula:
= 
= 
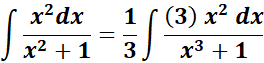
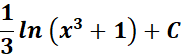
Exercises |
1. 
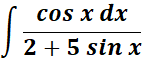
Steps:
a. Write the given 1st.
b. Use the specific logarithm integral formula.
c. Find the logarithm integral.
Solution:
=
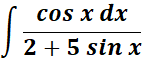
= Formula:
= u = sin x; du = cos x dx
= 
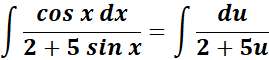
= a = 2; b = 5
= 
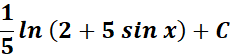
Answer: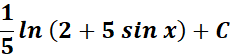
2. 
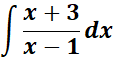
Steps:
a. Write the given 1st.
b. Use the specific inverse trigonometric integral formula.
c. Find the inverse trigonometric integral.
Solution:
=
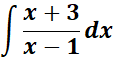
= Formula: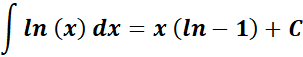
= Use Polynomial Long Division: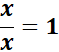 
= Then, multiply and subtract: (x - 1) .1 = x - 1
= Then, subtract: (x + 3) - (x - 1) = 4
= 
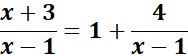
= New given: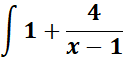 
= 
= 
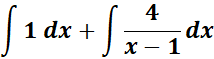
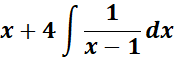
= x = x - 1
= 
Answer:
3. 
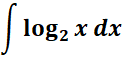
Steps:
a. Write the given 1st.
b. Use the specific logarithm integral formula.
c. Find the logarithm integral.
Solution:
=
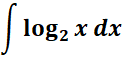
= Formula: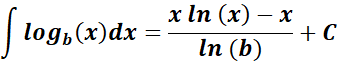
= Change it: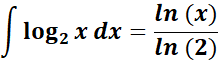 
= 
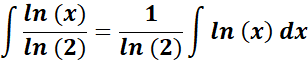
= u = ln (x); dv = dx; du = dx/x; v = x
= 
= 
= 
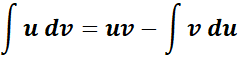
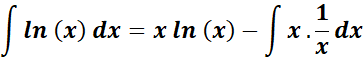
= Combine:
= 
= 
= 
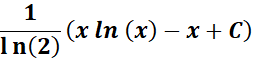
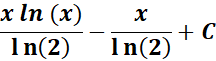
Answer:
4. 
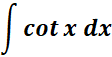
Steps:
a. Write the given 1st.
b. Use the specific logarithm integral formula.
c. Find the logarithm integral.
Solution:
=
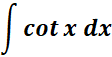
= Formula:
= Recall the trigo: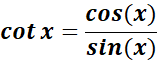 
= New Given: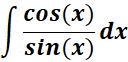 
= u = sin (x); du = cos (x) dx
= 
= 
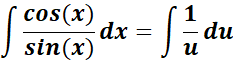
Answer:
5. 
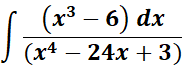
Steps:
a. Write the given 1st.
b. Use the specific logarithm integral formula.
c. Find the logarithm integral.
Solution:
=
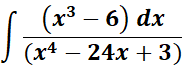
= Formula:
= u = x4 - 24x + 3; du = 4x3 - 24 dx; du = 4 (x3 - 6) = du
= 
= 
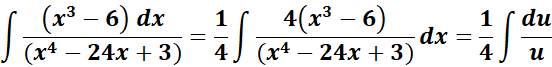
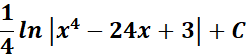
Answer: