Definition
Derivative of Exponential Function
-> The derivative of a exponential function depends on its base and exponent.
Symbol:
Where:
The a is the base, constant, a>0 and a not equal to 1.
The x is the exponent and variable.
Formulas of Exponential Derivatives |
1. Natural Exponential Function ex Rule
-> The property states that ex is the derivative itself.
Formula:
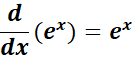
2. General Exponential Function ax Rule
-> The property involves multiplying the original function by the natural log of the base a, denoted by ln a.
Formula:
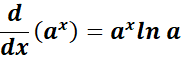
3. General Exponential Function with Nonlinear Argument au(x) Rule
-> The property involves the natural log of the base and the derivative of the exponent.
Formula:
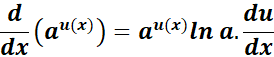
4. Exponential Function with a Linear Argument eax+b Rule
-> The property states the exponent is a linear function ax + b, the derivative involves the coefficient a of x.
Formula:
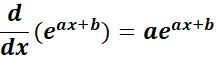
5. Exponential Function with a Constant Multiplier C.eu(x) Rule
-> The property tells the exponential function is multiplied by a constant C, the derivative retains this constant factor.
Formula:
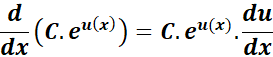
Example |
1. Find the answer from this given:
y = cos e3x
Steps:
a. Write the given and determine the value.
b. Use the specific Exponential formula.
c. Find the exponential derivative.
= y = cos e3x
= u = e3x; du = 3e3x
= 
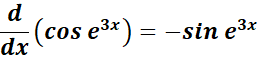
= - 3e3x sin e3x
Exercises |
1. y = e-3x
Steps:
a. Write the given and determine the value.
b. Use the specific Exponential formula.
c. Find the exponential derivative.
Solution:
= y = e-3x
= Formula: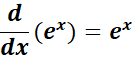
= u = -3x; du = -3
= 
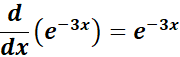
= -3 . e-3x
= -3e-3x
Answer: -3e-3x
2. g = 102t
Steps:
a. Write the given and determine the value.
b. Use the specific Exponential formula.
c. Find the exponential derivative.
Solution:
= g = 102t
= Formula: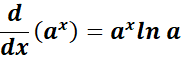
= u = 2t; du = 2
= a = 10
= 
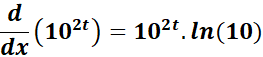
= 2 . 102t . ln(10)
= 2 ln 10 (102t)
Answer: 2 ln 10 (102t)
3. f = ln (5 - 4e4x)
Steps:
a. Write the given and determine the value.
b. Use the specific Exponential formula.
c. Find the exponential derivative.
Solution:
= f = ln (5 - 4e4x)
= Formula: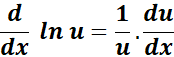 
= u = 5 - 4e4x; du = -16e4x
= 
= 
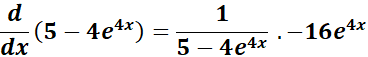
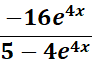
Answer: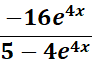
4. j = cos e-4x
Steps:
a. Write the given and determine the value.
b. Use the specific Exponential formula.
c. Find the exponential derivative.
Solution:
= j = cos e-4x
= Formula: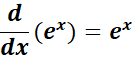
= u = e-4x; du = -4e-4x
= 
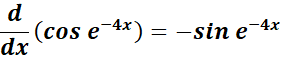
= -4e-4x . -sin e-4x
= 4e-4x sin e-4x
Answer: 4e-4x sin e-4x
5. k = a2 + a4 e-2 ln a
Steps:
a. Write the given and determine the value.
b. Use the specific Exponential formula.
c. Find the exponential derivative.
Solution:
= k = a2 + a4 e-2 ln a
= Formula: ;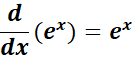
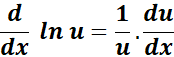
= u = a4; du = 4a3
= v = e-2 ln a; dv =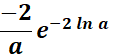 
= 2a +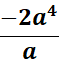 
e-2 ln a + 4a3 e-2 ln a
= 2a - 2a3 e-2 ln a + 4a3 e-2 ln a
= 2a + 2a3 e-2 ln a
= 2a (1 + 2a3 e-2 ln a)
Answer: 2a (1 + 2a3 e-2 ln a)