Definition
Derivative of Logarithmic Function
-> The derivative of a logarithmic function loga(x) with respect to x.
Symbol:
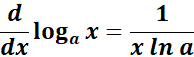
Where:
The a is the base of the logarithm and ln (a) denotes the natural logarithm of a.
Formulas of Log Derivatives |
1. Chain Rule
-> The property states compute the derivative of a composite function.
Formula:
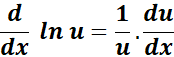
2. Log with Base a Rule
-> The property states calculates the derivative of the logarithm of ? with respect to ? where the logarithm has base ?.
Formula:
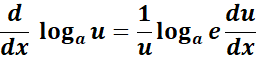
3. Log with Base u Rule
-> The property states the generalization of the derivative formula for logarithms with respect to a constant base.
Formula:
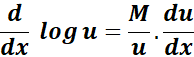
Example |
1. Find the answer from this given:
y = ln (5 - 3x)
Steps:
a. Write the given and determine the value.
b. Use the specific Log formula.
c. Find the log derivative.
= y = ln (5 - 3x)
= u = 5 - 3x; u = -3
=
= 
= 
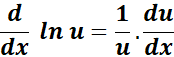
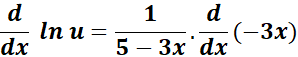
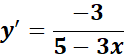
Exercises |
1. y = ln (cx)
Steps:
a. Write the given and determine the value.
b. Use the specific Log derivative formula.
c. Find the log derivative.
Solution:
= y = ln (cx)
= Formula: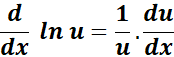
= u = cx; u = x
= 
= 
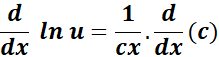
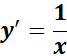
Answer: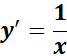
2. y ln x - x ln y = c
Steps:
a. Write the given and determine the value.
b. Use the specific Log derivative formula.
c. Find the log derivative.
Solution:
= y ln x - x ln y = c
= Formula: ;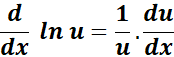 
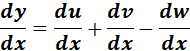
= u1 = y ln x; u1 =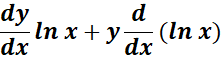 
; 
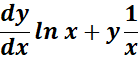
= u2 = - x ln y; u2 =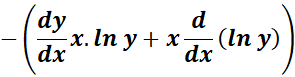 
; 
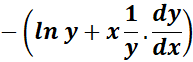
= c = 0
= 
= 
= 
= 
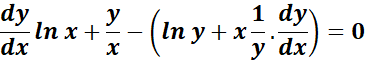
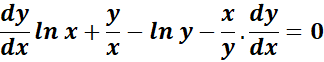
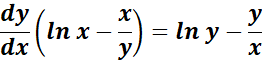
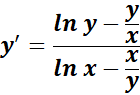
Answer: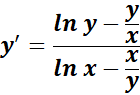
3. 
Steps:
a. Write the given and determine the value.
b. Use the specific Log derivative formula.
c. Find the log derivative.
Solution:
=
= Formula: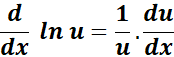
= u = 
; u =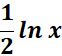 
= 
= 
= 
; 
= 
= 
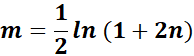
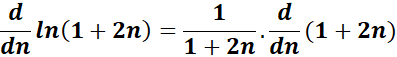
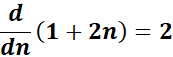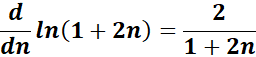
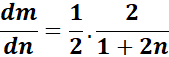
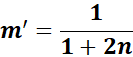
Answer: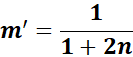
4. u = ln sec t
Steps:
a. Write the given and determine the value.
b. Use the specific Log derivative formula.
c. Find the log derivative.
Solution:
= u = ln sec t
= Formula: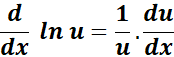
= 
= 
= 
= 
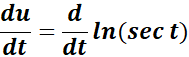
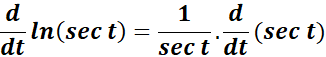
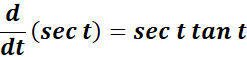
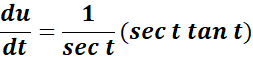
= tan (t)
Answer: tan (t)
5. w = z2 ln z
Steps:
a. Write the given and determine the value.
b. Use the specific Log derivative formula.
c. Find the log derivative.
Solution:
= w = z2 ln z
= Formula: ;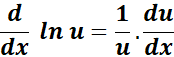 
= u = z2; u = 2z
= v = ln z; v = 1/z
= 
= 
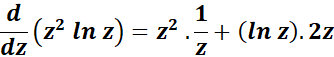
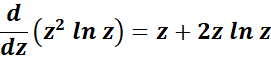
= z + 2z ln z
Answer: z + 2z ln z