| Properties of Logarithm |
Nov. 30, 2024, 11:47 a.m.
Definition
Logarithm
-> The logarithm of a number to a certain base, is the exponent to which the base is raised, to get said the number.
Exponential Function
-> The function of y = bx, where b > 0.
Properties of Logarithm |
1. Product Rule
-> The property states that logarithm of a product is equal to the sum of the logarithms of the factors.
Formula:
![]()
2. Quotient Rule
-> This property states that logarithm of a quotient is equal to the difference of the logarithms of the numerator and denominator.
Formula:
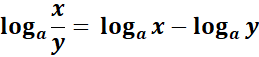
3. Power Rule
-> This property allows to bring the exponent inside the logarithm as a multiplier.
Formula:
![]()
4. Change of Base Formula Rule
-> The property states allows logarithms of any base to be converted into logarithms of any other base.
Formula:
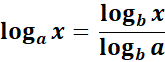
5. Log of 1 Rule
-> The property states logarithm of 1 to any base is always 0.
Formula:
![]()
6. Base Rule
-> The property states logarithm of the base itself to the same base is 1.
Formula:
![]()
7. Negative Rule
-> The property states logarithm of the reciprocal of x is equal to the negative of the logarithm of x.
Formula:
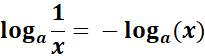
8. Exponentiation Rule
-> The property states logarithm of a number raised to an exponent is equal to the exponent.
Formula:
![]()
Example |
1. Find the answer from this given:
log5 (57)
Steps:
a. Write the given and determine the value.
b. Use the specific Logarithmic formula.
c. Find the Log.
= log5 (57)
= b = 5; x = 7
= 7 log5 (5)
= 7(1)
= 7
Exercises |
1. log2 (8) (4)
Steps:
a. Write the given and determine the value.
b. Use the specific Logarithmic formula.
c. Find the Log.
Solution:
= log2 (8) (4)
= Formula: ![]()
= x = 8; y = 4
= log2(8)(4) = log2(8) + log2(4)
= log2(8) = 3; log2(4) = 2
= log2(32) = 3 + 2
= 5
Answer: 5
2. 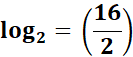
Steps:
a. Write the given and determine the value.
b. Use the specific Logarithmic formula.
c. Find the Log.
Solution:
= 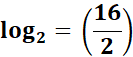
= Formula: 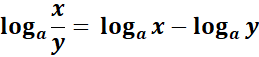
= x = 16; y = 2
= 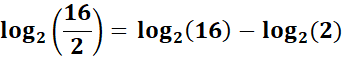
= log2(16) = 4; log2(2) = 1
= log2(8) = 4 - 1
= 3
Answer: 3
3. loga (2x - 5) + loga (x - 1) = loga 2
Steps:
a. Write the given and determine the value.
b. Use the specific Logarithmic formula.
c. Use the quadratic formula.
d. Find the x.
Solution:
= loga (2x - 5) + loga (x - 1) = loga 2
= Formula: ![]()
= loga (2x - 5) + loga (x - 1) = (2x - 5) (x - 1)
= loga 2 = 2
= (2x - 5) (x - 1) = 2
= 2x2 - 7x + 3 = 0
= 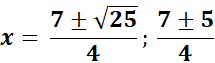
= 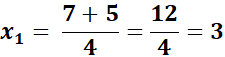
= 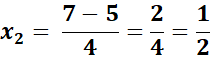
Answer: 3; 1/2
4. log5 (1)
Steps:
a. Write the given and determine the value.
b. Use the specific Logarithmic formula.
c. Find the Log.
Solution:
= log5 (1)
= Formula: ![]()
= log5(1)
= 50 = 1
= 0
Answer: 0
5. log10 (10)
Steps:
a. Write the given and determine the value.
b. Use the specific Logarithmic formula.
c. Find the Log.
Solution:
= log10 (10)
= Formula: ![]()
= a = 10
= 101 = 10
= 1
Answer: 1
