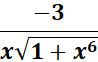Definition
Inverse Hyperbolic Functions
-> This tells the inverse of hyperbolic functions.
Formulas of Inverse Hyperbolic Functions |
1. Inverse Hyperbolic Sine Rule
-> The property tells inverse hyperbolic sine function returns the value whose hyperbolic sine is ?.
Formula:
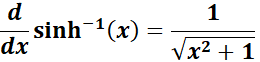
2. Inverse Hyperbolic Cosine Rule
-> The property tells inverse hyperbolic cosine function returns the value whose hyperbolic cosine is ?.
Formula:
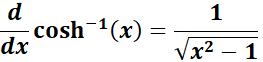
3. Inverse Hyperbolic Tangent Rule
-> The property tells inverse hyperbolic tangent function returns the value whose hyperbolic tangent is ?, where |x| < 1.
Formula:
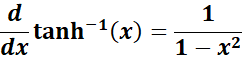
4. Inverse Hyperbolic Cotangent Rule
-> The property tells inverse hyperbolic cotangent function returns the value whose hyperbolic cotangent is ?, where |x| > 1.
Formula:
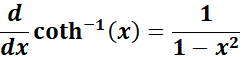
5. Inverse Hyperbolic Secant Rule
-> The property tells inverse hyperbolic secant function returns the value whose hyperbolic secant is ?.
Formula:
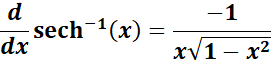
6. Inverse Hyperbolic Cosecant Rule
-> The property tells inverse hyperbolic cosecant function returns the value whose hyperbolic cosecant is ?.
Formula:
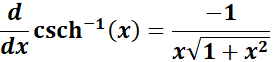
Example |
1. Find the answer from this given:
y = sinh-1 4x
Steps:
a. Write the given and determine the value.
b. Use the specific Inverse Hyperbolic derivative formula.
c. Find the inverse hyperbolic derivative.
= y = sinh-1 4x
= u = 4x; du = 4
=
= 
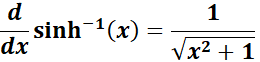
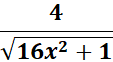
Exercises |
1. tanh-1 (2x + 1)
Steps:
a. Write the given and determine the value.
b. Use the specific general derivative formula.
c. Use the specific Inverse Hyperbolic derivative formula.
c. Find the inverse hyperbolic derivative.
Solution:
= tanh-1 (2x + 1)
= Formula: ;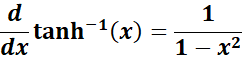 
= u = 2x + 1; du = 2
= 
= 
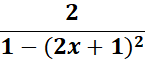
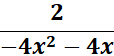
Answer: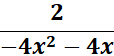
2. sech-1 (3x)
Steps:
a. Write the given and determine the value.
b. Use the specific general derivative formula.
c. Use the specific Inverse Hyperbolic derivative formula.
c. Find the inverse hyperbolic derivative.
Solution:
= sech-1 (3x)
= Formula: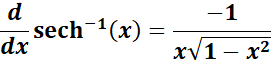
= u = 3x; du = 3
= 
= 
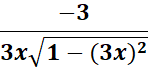
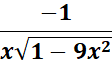
Answer: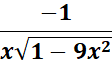
3. coth-1 (x2)
Steps:
a. Write the given and determine the value.
b. Use the specific general derivative formula.
c. Use the specific Inverse Hyperbolic derivative formula.
c. Find the inverse hyperbolic derivative.
Solution:
= coth-1 (x2)
= Formula: ;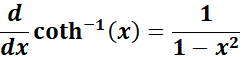 
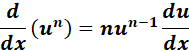
= u = x2; du = 2x
= 
= 
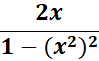
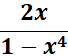
Answer: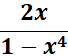
4. cosh-1 (x2 + 2x + 2)
Steps:
a. Write the given and determine the value.
b. Use the specific general derivative formula.
c. Use the specific Inverse Hyperbolic derivative formula.
c. Find the inverse hyperbolic derivative.
Solution:
= cosh-1 (x2 + 2x + 2)
= Formula: ;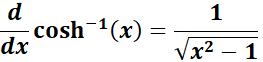
;
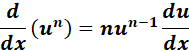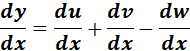
= u = x2 + 2x + 2; du = 2x + 2
= 
= 
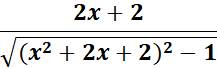
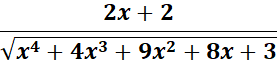
Answer: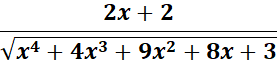
5. csch-1 (x3)
Steps:
a. Write the given and determine the value.
b. Use the specific general derivative formula.
c. Use the specific Inverse Hyperbolic derivative formula.
c. Find the inverse hyperbolic derivative.
Solution:
= csch-1 (x3)
= Formula: ;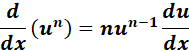
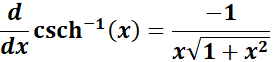
= u = x3; du = 3x2
= 
= 
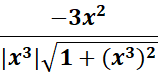
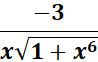
Answer: