Formulas of Derivative Hyperbolic Functions
1. Derivative of Hyperbolic Sine
-> The property states the hyperbolic sine is the hyperbolic cosine.
Formula:
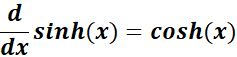
2. Derivative of Hyperbolic Cosine
-> The property states the hyperbolic cosine is the hyperbolic sine.
Formula:
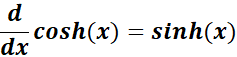
3. Derivative of Hyperbolic Tangent
-> The property states the hyperbolic tangent is the square of hyperbolic secant.
Formula:
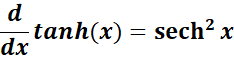
4. Derivative of Hyperbolic Cotangent
-> The property states the hyperbolic cotangent is the negative square of hyperbolic cosecant.
Formula:
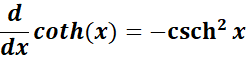
5. Derivative of Hyperbolic Secant
-> The property states the hyperbolic secant is the negative product of hyperbolic secant and tangent.
Formula:
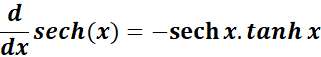
6. Derivative of Hyperbolic Cosecant
-> The property states the hyperbolic cosecant is the negative product of hyperbolic cosecant and cotangent.
Formula:
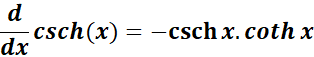
Example |
1. Find the answer from this given:
y = sinh 2x
Steps:
a. Write the given and determine the value.
b. Use the specific Hyperbolic derivative formula.
c. Find the hyperbolic derivative.
= y = sinh 2x
= u = 2x; du = 2
=
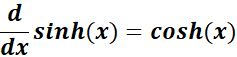
= cosh (2x) . 2
= 2 cosh (2x)
Exercises |
1. sinh x2
Steps:
a. Write the given and determine the value.
b. Use the specific general derivative formula.
c. Use the specific Hyperbolic derivative formula.
c. Find the hyperbolic derivative.
Solution:
= sinh x2
= Formula: ;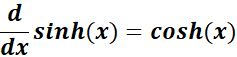 
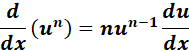
= u = x2; du = 2x
= cosh (x2) . 2x
= 2x cosh (x2)
Answer: 2x cosh (x2)
2. 
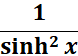
Steps:
a. Write the given and determine the value.
b. Use the specific general derivative formula.
c. Use the specific Hyperbolic derivative formula.
c. Find the hyperbolic derivative.
Solution:
=
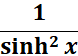
= Formula: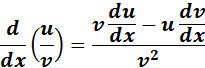 
;
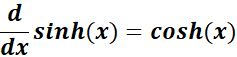
= u = 1; du = 0; v = ( sinh2(x) )2; dv = 2 sinh (x) . cosh (x)
= 
= 
= 
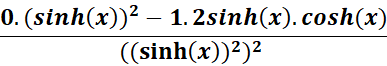
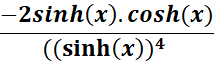
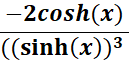
Answer: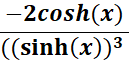
3. 
Steps:
a. Write the given and determine the value.
b. Use the specific general derivative formula.
c. Use the specific Hyperbolic derivative formula.
c. Find the hyperbolic derivative.
Solution:
=
= Formula: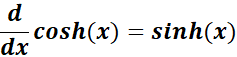
= u = u2; du = 2u; x = cosh (x); dx = sinh (x)
= 2 . cosh (x) . sinh (x)
= 2 cosh (x) sinh (x)
Answer: 2 cosh (x) sinh (x)
4. sinh5 x cosh5 x
Steps:
a. Write the given and determine the value.
b. Use the specific general derivative formula.
c. Use the specific Hyperbolic derivative formula.
d. Use specific hyperbolic identities.
e. Find the hyperbolic derivative.
Solution:
= sinh5 x cosh5 x
= Formula: ;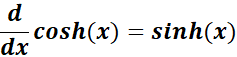
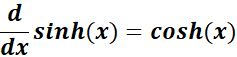
= u = sinh5 x; du = 5 sinh4(x) . cosh(x)
= v = cosh5 x; dv = 5 cosh4(x) . sinh(x)
= [ 5 sinh4 (x) . cosh (x) ] . cosh5 (x) + sinh5 (x) . [ 5 cosh4 (x) . sinh (x) ]
= 5 sinh4 (x) cosh6 (x) + 5 sinh6 (x) cosh4 (x)
= 5[( sinh4 (x) cosh6 (x) ) + ( sinh6 (x) cosh4 (x) )]
= sinh (2x) = 2 sinh (x) . cosh (x) and cosh (2x) = cosh2 (x) + sinh2 (x)
= 
= 
= 
= 
= 
= 
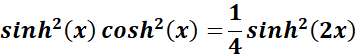
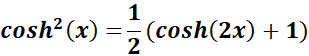
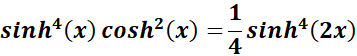
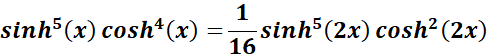
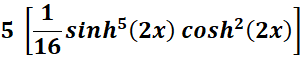
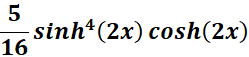
Answer: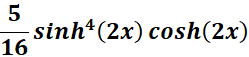
5. tanh (x2 + 3x)
Steps:
a. Write the given and determine the value.
b. Use the specific general derivative formula.
c. Use the specific Hyperbolic derivative formula.
c. Find the hyperbolic derivative.
Solution:
= tanh (x2 + 3x)
= Formula: ; ;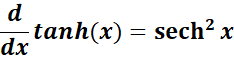 
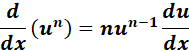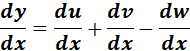
= u = x2 + 3x; du = 2x + 3
= v = tanh (u); dv = sech2 (u)
= sech2 (x2 + 3x) . 2x + 3
= sech2 (x2 + 3x) (2x + 3)
Answer: sech2 (x2 + 3x) (2x + 3)